На основании (4.10), (4.12) и (4.14) можно получить формулы для расчета кратности максимального и пускового моментов:

Л1п,ах = Л1шзх/Л1но =№ ом + 2/?1 + /?2Чом)/[2 (R,+ УШ]] \

(4.16)

Л1 . = Ж /Ж = (/?2/5 о + 2R, + /?.; s o )/(/?2+2/?1 + /?2). (4.17)

Сопротивления R и /?2 необходимо брать с учетом вытеснения тока в стержнях и насыщения.

Построение механической характеристики по круговой диаграмме. Для каждого положения точки А на круговой диаграмме (см, рис. 3.10) можно определить вра-щающий момент M = myi-AE и

Генераторный \ -v~ режим.

Режим злен/про нагнитнот ~ торможения

макс д1 двигатель ний режим

Рнс. 4.3, Зависимость электромагнитного момента н тока ротора от скольжения

скольжение s=PQ/PN (см. рис. 3,11, а), а затем, взяв ряд точек Л], Лг,... ,Л на окружности токов в пределах от точки О до точки К, построить зависимость М- =/(s) или, определив n2 = ni(l -

-S), построить зависимость П2 =

Максимальный момент Мтах можно найти, проведя прямую, параллельную линии ОТ и касательную окружности токов (см. рис. 3,11, а). Опустив перпендикуляр на диаметр окружности и? точки касания Ам, получим отрезок АмЕм, где £м -точка пере-сечения перпендикуляра с прямой ОТ. Очевидно, что Мтах= мХ У,АмЕм, так как отрезок АмЕ является максимальным расстоянием между окружностью токов и линией ОТ. Момент при s=l

(пусковой момент) определяется отрезком KR, умноженным на масштаб моментов.

Из (4,2) и круговой диаграммы видно, что при увеличении скольжения от s=0 до s=l ток ротора h монотонно возрастает, в то время как электромагнитный момент сначала увеличивается с ростом скольжения, достигает максимума при s = Skp, а затем уменьшается, несмотря на возрастание тока /2 (рис. 4.3).

Физически это объясняется тем, что в формуле момента М= =СмФт12cosHpi при малых скольжениях преобладающее влияние имеет возрастание тока /2. При увеличении скольжения свыше Skp ток /г увеличивается сравнительно мало и преобладающее влияние оказывает уменьшение созтрг; оно происходит вследствие

увеличения частоты тока в роторе /2=5/1. а следовательно, и сопротивления X2 = 2nf2L2.

Построение механической характеристики по каталожным данным. На практике широко используют приближенное аналитическое выражение механической характеристики.

Согласно (3.15) и (3.20), электромагнитный момент асинхронного двигателя

m = P 2KQs) = m/lR2KlS) = m2sElR2ll (rI + sxI). (4.18)

Принимая приближенно £2 const, т. е. считая, что магнитный поток машины при изменении нагрузки не меняется, и приравнивая нулю производную dM/ds, полученную из (4.18), можно найти критическое скольжение, соответствующее максимальному моменту: 5кр ±/?2Д2. и соответственно максимальный момент

М, ± mEl/(2QiX2). (4.19)

Разделив выражение (4.18) на (4.19), после преобразования получим

Л1/Ж з,2/(5,р/5 + 5/5кр)-

(4.20)

аналогично,

MjM 2s,l{\ + sl). (4.21)

При этом можно получить значения моментов М, Мщах и Мп в относительных единицах (т. е. в долях от базового момента М ом):

М = М/М = ( S o /Skp + SplS MslSp + 5кр/5);

, = тах/Лн о = (Shom/Skp I SjS )l2;

Л1п. = MjM = (S o /Skp 4- Sp/S o )/( 1/Skp + Skp)-

(4.22)

(4.23)

(4.24)

Более точные формулы для определения моментов асинхронного двигателя по каталожным данным можно получить на основе анализа Т-образной схемы замещения. Значения этих моментов в относительных единицах (т. е. в долях от базового момента М ом):

= М/М а = (S ом/5кр + кр/5ноч + 2р5кр)/(5/5кр + кр/ + 2р5кр);

(4.22а)

тах.= Л1 ах/Л1 нон -(*ном/*кр~Ь V oM + 2psKp)/12(l+PSKp)l; (4.23а) Ж .=MJM = (s <, /Skp + Skp/Shom + 2ps,p)/[ 1/Skp + Skp (1 + 2p)l. (4.24a) где p=Ri/CiR2.

Разделив (4.22а) на (4.23а), а также (4.24а) на (4.23а), получим:

Л/Лшах= [2 (1 + р5кр]/(5/5кр + кр/ + 2р5кр); (4-25)

Лп/Лп,ах = [2(1+Р5кр)ч1/11+4(1 + 2р)]. (4.26)

Отметим, что значение р мало влияет на скольжение кр. Для двигателей серии 4А и АИ основного исполнения с высотами оси

вращения 56... 132 мм можно пользоваться усредненным значением р=1,32. Во многих случаях пренебрегают членом 2ps p и тогда получают упрощенные выражения (4.20), (4.23) и (4.24) для

2,0 j t,0 0,5 О 5)

2,5 2,0 i,5 1,0 0,5

2,5 2,0 1,5 1,0 0,5 О

0,2 0,и 0,5 0,8 S

0,2 0,4- 0,5 0,8 S

Рис. 4.4. Механические характеристики некоторых асинхронных двигателей серии 4А: основное исполнение 37 кВт (а), основное исполнение 1,5 кВт (б), с повышенным пусковым моментом 30 кВт (в):

( - по (4.27) и (4.29). 2 -по (4.22). 3 -по (4.28), н (4.29), 4 - по опыту

построения механической характеристики.

Формулы (4.22) ... (4.24) являются приближенными и дают погрешности, так как не учитывают падение напряжения в обмотках статора. Особенно велика погрешность при переходе из двигательного режима в генераторный. Однако для исследования одного режима выведенные формулы дают приемлемую точность. Объясняется это тем, что в области малых скольжений от s=0 до s p магнитный поток изменяется незначительно и, следовательно, в этой области указанные формулы не могут дать большой погрешности, тем более что точки механической характеристики при s=0 и s p являются фиксированными.

При скольжении, близком к единице, эти формулы, казалось бы, должны давать завышенные значения момента, так как при больших токах сильнее сказывается падение напряжения в статоре. Однако в реальных машинах при скольжениях, близких к единице, уменьшаются сопротивления /?2 и Х2 из-за явления вытеснения тока в проводниках и насыщения коронок зубцов, что ведет к увеличению момента. В ре-

зультате оказывается, что погрешность, обусловленная пренебрежением падения напряжения в статоре, и погрешность, вызванная изменением параметров ротора, взаимно противоположны, вследствие чего точность указанных приближенных формул достаточна для практических целей. Еще большую точность дают формулы (4.22а) ... (4.26), которые учитывают сопротивление обмотки статора.

На основании изучения механических характеристик современных электродвигателей, снятых экспериментальным путем, можно сделать следующие выводы:

экспериментально полученные кратности максимального, минимального и пускового моментов примерно на 10% больше значений, установленных в ГОСТе. Поэтому формула механической характеристики должна основываться на относительных значениях моментов Мтах., Mmin. И Мп., установленных в ГОСТе;

точную формулу механической характеристики M=f(s), основанную на анализе схемы замещения с переменными параметрами, получить весьма трудно, поэтому лучше пользоваться формулой, полученной на основании опытных данных;

двигатели по виду механических характеристик можно условно разделить на две группы: с жесткими характеристиками (skp 0,15) и с мягкими характеристиками (Skp0,15);

механическую характеристику целесообразно разбить на две зоны. В первой зоне от s=l до Skp для всех современных коротко-замкнутых двигателей с беличьей клеткой, выполненной из алюминия, ее целесообразно аппроксимировать квадратичной зависимостью момента от скольжения, проходящей по точкам с координатами: (Мп., 5=1); (Mmln., Smin) И (Mmax., 5кр) , Т. С.

(4.27)

где ffo = Afn. -(ai4-a2)>0; ai= -202(02 -l-n - Amin )<0;

= (ог - КАп.-Af n,in.)/a2.

Для двигателей с двойной беличьей клеткой (см. § 5.3) зависимость момента от скольжения в указанной зоне целесообразно заменить прямой, проходящей через точки с координатами: (Мп.,

5=1) и (Мтах, 5кр), Т. С.

M=ao-\-ais,

(4.28)

где ао= (Мтах. -Мп.5кр)/(1-5кр)>0; ai=(Mn.-Мтах.)/(1 - -5кр)<0.

Во второй зоне от кр до s = 0 для двигателей с жесткими характеристиками, в том числе и для двигателей с двойной беличьей

клеткой, механическую характеристику целесообразно аппроксимировать линейной зависимостью

(4.29)

. = т ( / кр).

а для двигателей с мягкими характеристиками - квадратичной зависимостью:

и = И .-(Ж - 1) [(Skp-5)/(Skp-5kom)P-

(4.30)

На рис. 4.4 приведены механические характеристики некоторых двигателей, полученные по приведенным формулам и экспериментально, которые показывают, что принятая выше аппроксимация обеспечивает достаточную для практических целей точность.

4.2. Влияние на механическую характеристику высших гармоник магнитного поля

Причины, вызывающие возникновение высших гармоник магнитного поля. Магнитное поле в воздушном зазоре асинхронной машины несинусоидальное. В нем, кроме основной гармонической, существует бесконечно большое число высших гармоник поля, которые принято разделять на пространственные и временные.

Пространственные гармоники появляются вследствие несинусоидальности распределения МДС в воздушном зазоре, обусловленной дискретным расположением проводников обмотки в пазах, и неравномерности самого воздушного зазора, вызванного наличием зубцов на статоре и роторе и рядом технологических факторов (эксцентричностью ротора и статора, конусностью ротора, эллипс-ностью зазора и др.). От основной гармоники поля высшие пространственные гармоники отличаются тем, что они имеют значительно меньшую амплитуду, другое число периодов и другие частоты вращения.

Высшие пространственные гармоники создают ряд добавочных моментов, действующих на ротор и оказывающих влияние на механическую характеристику двигателя. Эти моменты подразделяют на асинхронные, синхронные, вибрационные и реактивные.

Временные гармоники поля появляются при питании двигателя несинусоидальным напряжением, например при питании его от статического преобразователя частоты, когда к обмотке статора подводится напряжение прямоугольной формы (см. § 6.2), или при включении в цепь обмотки статора нелинейных элементов (нелинейных реакторов, вентилей и др.). В этих случаях токи фаз содержат наряду с основной гармоникой и высшие гармоники, каждая из которых имеет частоту fv=v/i и создает такой же ряд пространственных гармоник, как и основные гармоники, но вращающиеся в v раз быстрее.

Гармоники, возникающие при питании двигателя несинусоидальным напряжением, создают добавочные асинхронные и колебательные моменты. Все виды высших гармоник (пространственные и временные) приводят к возникновению добавочных потерь мощности в обмотках и магнитопроводе машины.

Рассмотрим более подробно некоторые причины возникновения высших пространственных гармоник, создаваемые в результате несинусоидальности распределения МДС в воздушном зазоре.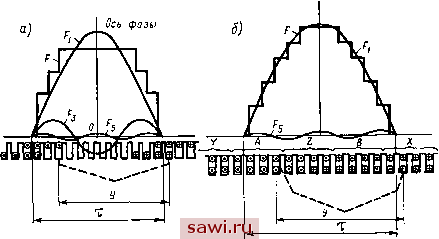

Рис. 4.5. Распределение МДС, создаваемой одной (а) и тремя (б) фазами трехфазной обмотки

Распределение МДС обмотки в симметричной машине представляет собой периодически изменяющуюся кривую, у которой при разложении в гармонический ряд отсутствуют четные гармоники. Применение обмотки с укороченным шагом улучшает форму распределения кривой МДС, но получить этим способом идеальную синусоидальную форму не представляется возможным. На рис. 4.5, а показана в качестве примера кривая МДС одной фазы трехфазной обмотки при q=4 и р==£ т=0,835, а на рис. 4.5, б - та же кривая для всей обмотки, полученная путем суммирования МДС каждой из фаз. Сравнивая эти кривые, можно установить, что форма МДС для всей обмотки заметно улучшается. При этом третьи гармоники, довольно сильно выраженные в кривой на рис. 4.5, а, в кривой на рис. 4.5, б взаимно уничтожаются.

В общем случае возникают гармоники порядка v = 2m/C+l, где К=0, 1, 2, 3... . Для трехфазной обмотки (/п = 3) v=6/C±l, т. е. образуются вращающиеся волны МДС при v= 1, 5, 7,11, 13,..., при этом исчезают гармоники с номерами, кратными трем. Так как полюсное деление v-й гармоники Tv в v раз меньше полюсного деления Ti первой гармоники, а частота ее f-fi, то образующиеся выс-