(рис. 5.9, а), заложенных в глубокие пазы ротора, высота которых в 6... 12 раз больше ширины. Такие стержни можно рассматривать как проводники, разделенные на большое число слоев. Из рис. 5.9, б видно, что нижние слои проводников сцеплены с большей частью потока рассеяния Фаг, чем верхние, и имеют соответственно большую индуктивность 1г.

В начальный момент пуска при s=l частота изменения тока в роторе большая и распределение тока по параллельным слоям определяется в основном их индуктивным сопротивлением. Поэтому при пуске происходит вытеснение тока в верхние слои (плотность тока Д по высоте проводника распределяется, как показано на рис. 5.9, в, кривая /), что равносильно увеличению активного сопротивления стержня и приводит к повышению пускового момента двигателя. При s - Saou частота тока f2=f\S в роторе мала (например, при /i = 50 Гц и 5 = 0,02 частота /г= 1 Гц) и соответственно меньше его индуктивное сопротивление Х2$. Вытеснения тока в этом случае не происходит; он распределяется приблизительно равномерно по высоте стержня (рис. 5.9, в, кривая 2). В результате резко уменьшаются активное сопротивление ротора и потери мощности АРал2. Одновременно изменяется поток рассеяния Фаг. а следовательно, и сопротивление Х2.

Изменение параметров R2 и Х2 глубокопазного двигателя в зависимости от величины скольжения приводит к тому, что его характеристика M = f{s) (см. рис. 5.8,6, кривая 2) близка к соответствующей характеристике двигателя с двойной беличьей клеткой (кривая 3). Здесь же для сравнения показана характеристика М = = f(s) для двигателей с короткозамкнутым ротором нормального исполнения (кривая /).

Круговая диаграмма. При построении круговой диаграммы для двигателей с двойной беличьей клеткой и глубоким пазом проводят дополнительно опыт короткого замыкания при пониженной частоте тока /пон (порядка 5 Гц) и пониженном напряжении Uu- Напряжение уменьшают пропорционально понижению частоты, так чтобы при значении Uk ток короткого замыкания / = (1,0... 1,5) X Х/ном. Полученные значения / и Рк приводят к номинальному напряжению по формулам

к.ном

ном/пон

к.ном к

(5.7)

По данным опытов холостого хода (с учетом рис. 3.13) и короткого замыкания [согласно формуле (5.7)] находят положение точек О и /Ci (рис. 5.10). Масштаб мощности при пониженной частоте для построения точки Ki равен масштабу мощности при номинальной частоте, умноженному на отношение /пон ном. Затем проводят линию 0/Ci и поворачивают ее по часовой стрелке на угол (oi-ог), получая точку /С/; при этом

Через точку Ki и точку О проводят окружность токов / с центром О], лежащим на линии 0L (диаметре окружности). Линию 0L проводят под углом 2у к горизонтальной линии ОВ, а линию моментов ОГ -под углом б к линии 0L, так же как в диаграмме (рис. 3.14).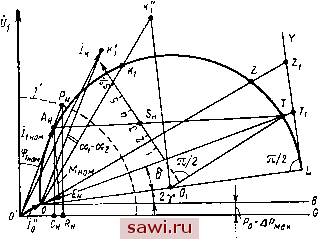

Рис. 5.10. Круговая диаграмма для двигателей с двойной беличьей клеткой и глубокопазных

Для построения линии полезной мощности 0Z из центра Oi окружности / восставляют перпендикуляр к линии 0L до пересечения в точке К\ с продолжением линии OKi. Затем из точки L восставляют перпендикуляр LY к прямой 0L и откладывают на нем отрезок LZ\ = 20iKi (}поя/!иои) Пересечение линии OZ, с окружностью токов / дает точку Z.

Для построения линии скольжения проводят радиус ОТ и из точки Т вдоль прямой ОТ откладывают отрезок TN, длина которого (см) 1= {T\ZxlOT\) 100. Через точку N проводят шкалу скольжения S (%) перпендикулярно радиусу 0\Т. Деления этой шкалы соответствуют масштабу 1 см=1%- Для определения коэффициента мощности проводят окружность Г из точки О радиусом 100 мм, так же как и при построении диаграммы (рис. 3.14).

Для проверки значений КПД. коэффициента мощности и скольжения при номинальном режиме определяют на окружности токов / положение точки А , соответствующей номинальному режиму работы двигателя. Для этого откладывают на диаграмме электромагнитную мощность Рзм. соответствующую номинальному моменту Мном, в виде отрезка Лнн. перпендикулярного линии ОВ, от окружности / до линии моментов ОТ (можно так же выразить ЛГном в Н-м с соответствующей корректировкой масштаба). Значение

этой мощности вычисляют по формуле р9 1.но 1= {Р2 + АРиех +

+ДРд) (rei/re2H0M), где Р2, ДРмех и ДРд относятся к номинальному режиму.

Для определения коэффициента мощности при номинальном режиме проводят линию ОА и продлевают ее до точки Рн на окружности Отрезок Рн/?н (мм), поделенный на 100, дает значение со5ф1ном. Для определения скольжения при номинальном режиме проводят линию АпТ; точка S пересечения этой линии со шкалой скольжения дает значение скольжения Shom (%) Потребляемая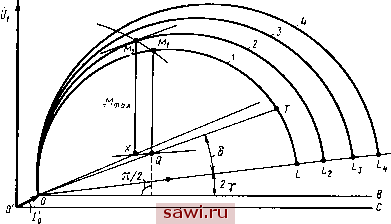

Рис. 5.11. Определение по круговой диаграмме максимального момента

мощность в рассматриваемом режиме выражается отрезком А Св. КПД подсчитывают по отдельным потерям; при этом электрические потери ДРэл! и ДРэлг в обмотках статора и ротора определяют по величинам тока и скольжения, полученным из круговой диаграммы. Магнитные и механические потери находят из опыта холостого хода (см. рис. 3.13), а добавочные определяют экспериментально или принимают условно, равными 0,5% от Ргном (для двигателей мощностью до 100 кВт).

Для определения максимального момента с учетом насыщения в рассматриваемой круговой диаграмме делают дополнительные построения (рис. 5.11). Для этого находят положения точек Кз и К*, которые совместно с точкой О позволяют начертить окружности токов 3 н 4 с центрами, лежащими на прямой 0L. Точку Кз определяют по данным опыта короткого замыкания, проводимого при номинальной частоте и токе /к = /ном, а точку /С* -по данным опыта короткого замыкания, проводимого при номинальной частоте и токе /н= (2,5... 4) /ном. Полученные значения / и Рн приводят к но-

минальному напряжению, так же, как и при построении окружности токов / на рис. 3.14.

Диаметр окружности токов 2, служащей для определения максимального момента, определяют по формуле 012= 0L {OLJOL3). Линию моментов ОХ для окружности токов 2 строят так же, как и в круговой диаграмме (рис. 3.17). Отрезок М2Х дает значение максимального момента Afmax.

Существуют разновидности глубокопазиых двигателей с трапецеидальной, двухступенчатой и колбообразной формами поперечного сечения стержней (рис. 5.12, а). Двигатели с глубокими пазами на роторе несколько дешевле двигателей с двойной беличьей клеткой, но последние более надежны в работе, так как механические напряжения у основания зубцов у них меньше, чем в глубокопазиых двигателях.

Кппмр тпгп ич-чй увеличения 5.12. Формы поперечного сече-

дроме того, из за увеличения ержией обмотки ротора асии-магнитного потока рассеяния ро- хронных двигателей тора глубокопазные двигатели

имеют несколько уменьшенный созф, при номинальном режиме и обладают пониженной перегрузочной способностью км-

Изменение параметров обмотки ротора из-за вытеснения тока. Явление вытеснения тока при пуске и связанное с этим увеличение активного и уменьшение индуктивного сопротивлений имеет место (в меньшей степени) и в двигателях с короткозамкнутым ротором нормального исполнения. Поэтому определение пусковых характеристик по круговой диаграмме носит приближенный характер, как и сама диаграмма, построенная в предположении неизменности основных параметров двигателя. С целью усиления эффекта вытеснения тока в современных короткозамкнутых двигателях мощностью до 100 кВт пазам ротора и стержням беличьей клетки придают специальную сильно вытянутую форму (рис. 5.12,6). В этом случае при определении активного и индуктивного сопротивлений обмотки ротора необходимо учитывать явление поверхностного эффекта.

Для учета вытеснения тока в процессе пуска двигателя вводятся понятия эквивалентной глубины проникновения Лщ, тока в стержень обмотки ротора и приведенной высоты стержня l=h/h p, где А - действительная высота стержня.

Активные и индуктивные сопротивления обмотки ротора с учетом вытеснения тока

/?П = *Я2п + /?2л; X2i = kx2n + X2 (5.8)

где Rza, Х2п - активное и индуктивное сопротивления пазовой части обмотки (окруженной сталью) при равномерном распределении тока по сечению ее стержней; /?2л, 2л -то же, лобовых частей.

На основании проведенных исследований [8] установлено, что коэффициенты, учитывающие изменение сопротивлений Яп и Хгп из-за вытеснения тока, могут быть представлены в виде

ft;j=S(sh 2S + sin 2S)/(ch 2$ -cos 2$); (5.9)

ftx = 3 (sh 2S- sin 2Щ2 (ch 2- cos 2$)]. (5.10)

Зависимость коэффициентов и kx от приведенной высоты стержня I представлена на рис. 5.13, а. В рабочем диапазоне (g = = 1... 4) в (5.9) и (5.10) можно пренебречь тригонометрическими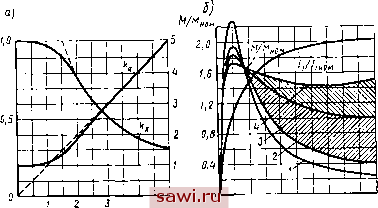

0,2 0,4 0,Б 0,6 1,0 S

Рис. 5.13. Зависимости коэффициентов kn и kx от приведенной высоты стержня (а) и механические характеристики двигателей с пазами ротора различной формы (б)

функциями sin2g и cos2g по сравнению с гиперболическими sh2g и ch2g и принять sh2g = ch2. При этом указанные выражения можно аппроксимировать зависимостями я = и = 3/(2) (показаны на рисунке пунктиром). Эквивалентная глубина проникновения тока в стержень

(5.11)

flnp = V2l(2),

где l=lo - магнитная проницаемость материала стержня; у - его удельная проводимость; шг - угловая частота тока в обмотке ротора. Следовательно, чем больше частота тока в роторе и удельная проводимость материала стержня, тем сильнее сказывается эффект вытеснения тока.

Приведенная высота стержня при ц = цо = 4я-10- и Ш2=2я/2= = 2nfis

k = hy (со21лу/2) Ф1Ь )= 2nh VyfisфЮ 10-. (5.12)

Здесь отношение ширины стержня b к ширине паза Ьп учитывает возможное неполное заполнение паза стержнем, которое экви-

валентно уменьшению удельной проводимости у. При частоте тока в обмотке статора 50 Гц и литой беличьей клетке {b = bn) выражение (5.12) принимает вид

S=1,4-10-2A1/ys.

(5.13)

Если выразить высоту Л в см, то для медных стержней (р= 11у= = 0,02-10-6 Ом/м при 50°С) имеем l = hVs; для беличьей клетки, залитой алюминием, -=0,7/i Ys при расчетной температуре 75°С и 5=0,66Л Vs при температуре 115°С. У медных стержней вытеснение тока начинает оказывать влияние на значение сопротивлений Ria и Хгп при Л>1 см, а у алюминиевых - при Л>1,4 см. Для роторов, залитых алюминием, с высотой паза более 35 мм эквивалентная глубина проникновения тока в стержень при пуске (s=l) и расчетной рабочей температуре 115°С составляет 15 мм. В двигателях с глубокими пазами при высоте стержня 5 см активное сопротивление пазовой части стержня в результате вытеснения тока в начальный момент пуска (s=l) возрастает в 5 раз, а индуктивное-уменьшается в 3,3 раза по сравнению с их значениями при рабочем режиме.

Изменение сопротивлений Rz и Х2 обмотки ротора в процессе пуска двигателя оказывает существенное влияние на форму механической характеристики. На рис. 5.13,6 приведены несколько механических характеристик двигателей с пазами ротора (т. е. со стержнями беличьей клетки) различной формы. Кривая / относится к двигателям с круглыми пазами. Зону между кривыми 2 и 3 занимают двигатели с трапецеидальными пазами и глубокопазные; между кривыми 3 и 4 - двигатели с двойной беличьей клеткой и пазами колбообразной формы.

В микродвигателях размеры пазов ротора обычно настолько малы, что использование эффекта вытеснения тока оказывается невозможным.

5.4. Динамика пуска

Время разгона. Динамические свойства электропривода с асинхронным электродвигателем определяются уравнением

дии1

(5.14)

где Л1д = /йЙ2 -динамический момент системы асинхронный двигатель - производственный механизм.

Выражая момент инерции через маховой момент J=GD/4g (кг-м) (g - ускорение силы тяжести, равное 9-81 м/с) и частоту вращения Я2=2ял2/60, получим

d/i2

(5.15)