Математический аппарат, используемый для оптимального проектирования серии асинхронных двигателей, - нелинейное программирование. Оно позволяет оптимизировать нелинейные функции с линейными и нелинейными ограничениями.

Задачей нелинейного программирования является определение некоторого л-мерного вектора in>0, который при изменении п независимых переменных минимизирует или максимизирует функцию:

F(jc )=min;

jCi>0; г= 1,..., п.

(10.1)

Нелинейная функция п переменных F{xn), которую требуется оптимизировать (минимизировать или максимизировать), называется целевой функцией.

Если электрическая машина имеет узкоспециализированное назначение, то оптимальное значение целевой функции формулируется в техническом задании на проектирование. Им могут быть максимальные мощность, вращающий момент, КПД, cos ф, минимальные длина, масса, расход меди и т. д. Для машин общего назначения критерий оптимальности должен отражать народнохозяйственную эффективность от применения данной машины. Таким критерием обычно являются минимальные приведенные затраты на изготовление и эксплуатацию машины.

Вектор независимых леременных ж , от которого зависит значение целевой функции, содержит варьируемые при расчете машины величины, например геометрические размеры, электромагнитные нагрузки, качество изготовления и др. Линейные ил нелинейные функции fi(xn), значения которых не должны быть больше (или меньше) определенных заданных величин, называют ограничениями или лимитерами. При проектировании электрических машин ими могут быть требования потребителей в части допустимых превышений температуры обмоток или других частей машины, энергетических показателей, максимальный момент, начальные пусковые ток и момент, а также некоторые размеры активной части, накладываемые конструкцией и технологией изготовления машины.

Задачей оптимального проектирования является установление таких значений вектора ж и его составляющих, при которых целевая функция принимает оптимальное значение.

Практически поиск оптимального варианта выполняется с помощью ЭВМ.

Задаче нелинейного программирования можно дать геометрическую интерпретацию. Например, если целевая функция Р (ii, хг) определяется двумя независимыми переменными х\ и х2, то ее можно выразить в виде ряда кривых на плоскости хи х2 (рис. 10.1, а), каждая из которых соответствует некоторому постоянному значению целевой функции. Эти кривые называют линиями уровня. 06-

ласть допустимых значений х ограничивается осями координат и кривой /i(ii, 2)0, определяющей наложенные ограничения. Оптимальное (минимальное) значение целевой функции при заданных ограничениях соответствует оптимальной точке х*, лежащей на границе допустимой области.

В допустимой области R целевая функция может иметь один или несколько экстремумов. В первом случае функция называется унимодальной, во втором - мультимодальной. Локальное оптимальное решение-наименьшее значение функции F{хп) в окрестности оптимальной точки. Глобальное оптимальное решение-наименьшее значение функции F{xn) для всех хп, находящихся внутри допустимой области R. В случае унимодальной целевой функции глобальное и оптимальное решения совпадают.

/!ити уро8ней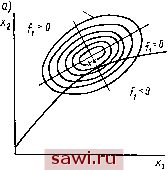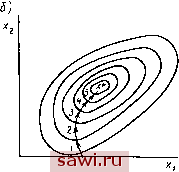

Рис. 10.1. Геометрическая интерпретация задачи нелинейного программирования

В зависимости от правил обхода допустимой области изменений целевой функции методы нелинейного программирования подразделяются на три группы: перебора, локального поиска и глобального поиска.

В методах перебора правило перехода от одной точки, соответствующей некоторым значениям независимых переменных, к другой точке задается заранее и не зависит от поведения целевой функции. Оно может быть детерминированным (метод перебора) или случайным (метод Монте-Карло). Эти методы гарантируют нахождение оптимума целевой функции с точностью до шага между отдельными точками (метод полного перебора) или с заданной вероятностью (метод Монте-Карло). Методы перебора требуют затраты значительного машинного времени и находят практическое применение только при небольшом числе независимых переменных (три-четыре).

В методах локального поиска переход от одной точки к другой осуществляется в зависимости от поведения целевой функ-

ции в окрестности предыдущей точки. К этим методам относятся: метод Гаусса - Зейделя, градиентные детерминированные in градиентные стохастические методы. Градиентные методы позволяют получить максимальное изменение целевой функции на каждый шаг, т. е. при движении точки в направлении градиента (рис. IO.I, б). Они дают возможность свести к минимуму число проб, гарантирующее нахождение оптимума с заданной точностью.

Приметодах глобального поиска сначала оценивают общие характеристики целевой функции в окрестности оптимума, а затем по ним находят глобальный оптимум. К методам глобального поиска относятся: метод множителей Лагранжа; метод, основанный на использовании теории плакирования экспериментов, и ряд других статистических методов.

Более подробно вычислительные методы нелинейного программирования, применяемые при оптимальном проектировании асинхронных двигателей, рассмотрены в [13].

Для современных программ оптимального проектирования характерно сочетание нескольких методов, которые попеременно включаются в работу в зависимости от поведения целевой функции, этапа поиска, требований к точности определения координат оптимальной точки и допустимого времени поиска. В начальной стадии поиска при значительном изменении целевой функции достаточно использовать простые статистические методы, имеющие большую дисперсию, но обладающие значительной скоростью счета. При выходе в существенно нелинейную область обычно используется метод статистического градиента или наилучшей случайной пробы. Последний метод заключается в проведении серии пробных шагов, из которых выбирается наилучший. При этом вероятность пропуска направления градиента невелика. При выходе в окрестность экстремума успешно применяется один из градиентных методов.

При проектировании двигателей серии АИ для определения геометрии активной части применялся метод случайного поиска с самообучением, при котором информация о поведении целевой функции в предыдущих точках используется для определения наивыгоднейшего направления следующего шага. При этом увеличивается вероятность выбора более удачного направления. Для уменьшения дисперсии ошибки случайные пробные шаги заменяют шагами, вычисленными на основе теории планирования экспериментов. Планирование эксперимента позволяет уменьшить число пробных точек по сравнению с градиентными методами.

Применяемые вычислительные методы позволяют с некоторым приближением определить экстремум целевой функции. Возникающие при этом ошибки можно уменьшить путем минимизации вместо критерия оптимальности некоторых варьируемых параметров двигателя, например длины сердечника. При этом удается уменьшить этот параметр без существенного изменения целевой функции.

Рассматриваемая методика оптимального проектирования является универсальной- пригодной для проектирования машин раз-

личных модификаций и исполнений (защищенное и закрытое, с короткозамкнутым и фазным ротором, с различной формой пазов, с различными видами обмоток и др.).

10.2. Установление критериев оптимальности

Выбор критериев. Задача оптимального проектирования серии асинхронных двигателей является многокритериальной. В качестве основного критерия при проектировании двигателей серий 4А и АИ принимался критерий минимума приведенных суммарных затрат (Зт), учитывающих стоимость изготовления двигателей и расходы на их эксплуатацию за нормативный срок окупаемости. Кроме поиска оптимальных параметров двигателей по этому основному критерию осуществляется также поиск по минимуму длины сердечника статора как показателя технологичности конструкции. При использовании методов нелинейного программирования представляется возможным осуществлять проектирование серии или отдельных машин по другим критериям оптимальности: максимуму полезной мощности, минимальной стоимости машины, минимуму массы, максимальным энергетическим показателям и др.

Составляющие критерия минимума суммарных приведенных затрат. Суммарные приведенные затраты на изготовление и эксплуатацию асинхронных двигателей можно выразить следующим образом:

3t={C, -\-C,)(1-\-T p,) + CJ (10.2)

где Сдв - производственная себестоимость двигателя, включающая в себя затраты на разработку, внедрение, изготовление и монтаж двигателя; Ср - стоимость устройств для компенсации реактивных токов; Са - годовые затраты на активные потери электроэнергии; Тн - нормативный коэффициент окупаемости, равный 1/Ея {Ев - нормативный коэффициент эффективности капитальных вложений); Ро - относительные затраты по обслуживанию и амортизационные отчисления. При проектировании серий двигателей 4А и АИ значение принималось равным 0,15; относительные затраты на обслуживание при эксплуатации - 0,069, а на амортизационные отчисления -0,065, т. е. суммарно ро = 0,134.

При установлении производственной себестоимости двигателя учитывают затраты на материалы, полуфабрикаты и покупные изделия; основную заработную плату производственных рабочих, отчисления на социальное страхование; накладные цеховые, общезаводские расходы и расходы на сбыт продукции (упаковку, транспортировку и пр.). Затраты на разработку и внедрение (научно-исследовательские и опытно-конструкторские работы, разработка технологии, изготовление оснастки, техническое перевооружение предприятий, освоение производства и др.) приближенно принимают равными 10% от производственной себестоимости двигателей. Затраты на монтаж двигателей при проектных и экономических

расчетах включают в затраты на их приобретение; в среднем их принимают равными 0,3 от цены двигателя.

Затраты на активные потери энергии (руб/год)

С, = з/АзР2(1 + Д;;з-71р)/71р, (Ю.З)

где Дэ=0,02 руб/(кВт-ч) - средняя цена электроэнергии; < -годовая наработка двигателя (число его часов работы в год); кз - коэффициент загрузки двигателя (расчетная нагрузка в долях от номинальной мощности); ДРэ = 0,04 -средние удельные потери на 1 кВт-ч передаваемой электроэнергии в пределах одной ступени трансформации; т]р-КПД двигателя при расчетной загрузке.

Проведенными исследованиями установлено, что для электродвигателей мощностью до 100 кВт средняя статистическая нагрузка составляет 60% от номинальной. Средняя годовая наработка в общем случае зависит от мощности двигателя, т. е. от его высоты оси вращения Я. В результате изучения условий эксплуатации асинхронных двигателей в СССР установлено, что годовую наработку i можно принять в соответствии с табл. 10.1.

Таблица 10.1

Эти значения кз и t были положены в основу оптимизационных расчетов при проектировании двигателей серии АИ. Однако для ряда отраслей промышленности (текстильная и др.), у которых электроприводы имеют среднюю годовую наработку более 3 тыс. ч, в серии АИ предусмотрено специальное исполнение двигателей. Расчеты показали, что такие двигатели целесообразно выполнять с повышенными значениями КПД и созф] путем увеличения длины пакета магнитопровода.

Для приближенных расчетов среднюю годовую наработку двигателя можно принять равной

/ = 545+ 3767. (10.4)

Эта формула для двигателей мощностью 10...100 кВт дает t = = 1250...1770 ч.

Затраты на компенсирующие устройства по методике ВНИИЭМ принимают

Cp=UpKsxJKP2 (tg =Рр - tg срн) (1 + Г Ро)/71р, (10.5)

где Яр=13 руб/(кВ-Ар-ч)-стоимость 1 кВ-Ар-ч компенсирующих устройств; А:тахн=0,25-коэффициент участия электродвигателей в максимумах нагрузки в системах электроснабжения; созфр - коэффициент мощности при расчетной нагрузке 0,6Рном; созфн=0,9 - нейтральный коэффициент мощности, при котором потребитель не платит штрафа и не получает премии; т]р - КПД при расчетной загрузке.

Дополнительные потери мощности, обусловленные потреблением реактивной энергии,

ДРр= Дрр (tg срр- tg *32/lp. (10.6)

где Арр - удельные потери на генерирование и передачу 1 кВ.Ар реактивной энергии (в этом случае Арр=0,11 кВт/(кВ.Ар)) или удельные потери, связанные с компенсацией 1 кВ.Ар посредством компенсирующих конденсаторных устройств (в этом случае Арр= = 0,085 кВт/(кВ.Ар)). Величина АРр может рассматриваться как собственные потери двигателя. Суммарные потери, включая значение АРр, называют приведенными, а КПД, вычисленный с учетом этих потерь,- приведенным КПД

71= 7i/Il + APp(tg=p-tg =? )!. (10.7)

Сопоставление значений приведенного КПД позволяет довольно просто сравнивать энергетические показатели двигателей одинаковой или близкой мощности.

Для учета компактности двигателя в затраты (Сдв+Ср) на изготовление двигателя и компенсирующих устройств могут быть включены затраты Сномп на необходимые производственные площади. Показателем компактности двигателя может служить отношение его номинальной мощности (кВт) к объему (м) описанного прямоугольного параллелепипеда (без учета выступающего конца вала)

*ком ~Я2/[4/У2(/-01, (10.8)

где Н - высота оси вращения, м; / и /в - габаритная длина двигателя и длина выступающего конца вала, м.

Стоимость производственной площади (Сил), необходимой для размещения двигателя, приблизительно можно определить по формуле

C , = 0.4B(/-/ )Z/ (10.9)

где В 2,5+1,9 lgP2 -эмпирически полученное уравнение регрессии размера станка (м) на стороне крепления двигателя от его номинальной мощности, кВт; /(пл=80... 100 - средняя стоимость производственной площади, руб/м2. При оптимальном проектировании может учитываться стоимость только части производственной площади, определяемая изменением компактности двигателя:

Скомп=0.4ВДЩ, (10.10)

где А/ - изменение габаритной длины двигателя.