Долговечность двигателей характеризуется гамма-процентным ресурсом {Ту), т. е. наработкой машины до первого отказа с веро-яностью Y (%).

Исходя из условий эксплуатации двигателей в номинальном режиме при температурах, близких к предельно допустимым для принятого класса нагревостойкости системы изоляции, гамма-процентный ресурс асинхронных двигателей установлен 20 тыс. ч; он определяется техническим ресурсом обмотки статора. На рис. II.2 показаны кривая изменения вероятности безотказной работы от времени t. Гамма-процентный ресурс определяется как время работы двигателя Ту при установленном значении у {%).

Для двигателей серии 4А гамма-процентный ресурс составляет 20 тыс. ч с вероятностью 0,8 ...0,85, а для двигателей серии АИ - с вероятностью 0,9. Указанные показатели надежности и долговечности гарантируются заводами-изготовителями при условии эксплуатации двигателей в режимах, близких к номинальным в части температуры, числа пусков, условий окружающей среды, механических воздействий и др., а также при обеспечении надлежащей защиты от перегрузок и других аварийных режимов и соблюдении правил эксплуатации и технического обслуживания.

11.3. Математические модели надежности обмотки статора

Обмотка статора асинхронного двигателя с точки зрения надежности является системой, элементы которой соединены последовательно и резервирование отсутствует. Поэтому вероятность Ров (О безотказной работы обмотки за время i равна произведению вероятностей безотказной работы Рв {t) межвитковой, Рм{0 межфазной и Рк(0 корпусной изоляций:

PM=Psit)PA)PAi)- (11.10)

Составляющие (11.10) зависят от надежности элементов соответствующего вида изоляции. За элемент витковой изоляции принимается изоляция между парой соседних витков, за элемент корпусной-изоляция одного паза или его части, за элемент межфазной- изоляция межфазной прокладки или ее части.

Расчетные и экспериментальные исследования показали, что вероятность безотказной работы межфазной и корпусной изоляции значительно выше, чем витковой. Так, например, для наработки т= = 10 тыс. ч имеем Р (О Ям (О =0,999, а для т=20 тыс. ч. -Р (ОХ ХРм(0 =0.995. Поэтому при выполнении расчетов надежности всыпной обмотки можно ограничиться расчетом надежности витковой изоляции, выполнив затем соответствующую корректировку расчетов.

Для обмоток асинхронных двигателей разработаны две математические модели надежности. Обе они основаны на известной в теории надежности модели прочности , связывающей случайную

величину прочность со случайной величиной нагрузка . В первой математической модели в качестве параметра, характеризующего прочность изоляции , принято пробивное напряжение Unp элемента изоляции, а за нагрузку принимают приложенное к элементу электрическое напряжение Ua- Во второй модели прочность изоляции характеризуют ее дефектностью (количеством дефектов на единицу длины или площади). Элементами межвитковой изоляции считаются два проводника, расположенные рядом в пазу или в лобовой части обмотки и разделенные изоляционным промежутком. Для безотказной работы обмотки необходимым условием является исправность всех входящих в нее элементов, так как пробой изоляции между парой соседних проводников приводит к отказу всей обмотки. При этом предполагается, что все элементы обмотки одинаковы и отказывают независимо друг от друга.

При рассмотрении первой модели для витковой изоляции исходят из того, что отказ произойдет тогда, когда напряжение Uu, приложенное к сосед- цз графическая интер-НИМ проводникам, превышает пробив- претация математической мо-ное напряжение Uup межвитковой изо- дели надежности межвитковой ляции в данном месте. Следовательно, изоляции: (1/в) - плотность вероятность Рз того, что элемент витко- РрГж=\ежду =и: вой изоляции не выйдет из строя, будет f([/.)-плотность распределе-равна вероятности, что его пробивное ния пробивных напряжений напряжение Uup, характеризующее

электрическую прочность изоляции, превосходит приложенное к данному элементу коммутационное перенапряжение Ln. Приложенное и пробивное напряжения -случайные величины. Поэтому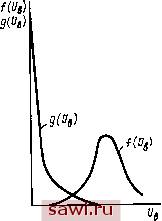

,(np>J = j/( )g-( )

(11.11)

где Дв) и g{UB)-соответственно плотности распределения пробивного и приложенного напряжений; Lb -напряжение, воздействующее на витковую изоляцию.

На рис. 11.3 приведена графическая интерпретация приведенной математической модели.

Длялюбого значения приложенного напряжения Uu с плотностью распределения вероятности (в) вероятность того, что пробивное напряжение Uup обмотки, состоящей из п элементов, превысит напряжение Uu, равна

(11.12)

где F{Ub)-функция распределения пробивного напряжения меж-витковой изоляции.

Формула (11.12) выражает математическую модель надежности межвитковой изоляции обмотки, состоящей из п пар проводников. Вычисление надежности по (И.И) и (11.12) требует определения соответствующих плотностей распределения напряжений fiVs) и g(VB) в аналитическом виде и их интегрирования. Точность вычислений зависит от соответствия принятых допущений реальным физическим процессам в изоляции обмотки, точности аппроксимации экспериментальных данных аналитическим выражениям Рис. 11.4. Кривые плотности распределения и пр.

пробивных наприжений витковой изолиции: pjg pj, 11 4 В качестве

/ - для новой изоляции. 2 - после установленной L 1 .

наработки (после ускоренных испытаний) ПрИМСрЗ ПрИВедСНЫ КрИВЫС

плотности распределения пробивных напряжений f(V ) для обмотки статора одного из серийных двигателей мощностью до 100 кВт с эмалевой витковой изоляцией. Наиболее часто для описания распределения пробивного напряжения элементов изоляции используют закон Вейбулла

Р{и,)=\~ехр{-и1/и). (11.13)

/2 1Ul/g,KB

При этом плотность распределения

Uq j

(11.14)

где а, Uq - параметры распределения, зависящие от воздействующих факторов и времени.

Соответствие этого закона эмпирическим кривым было проверено несколькими методами на большом числе статоров асинхронных двигателей и показало хорошее совпадение. При этом, как видно из рис. 1.14, в процессе эксплуатации происходит довольно существенное изменение зависимостей fiUs), так как по мере старения изоляции в ней начинают преобладать микроучастки с низким пробивным напряжением.

Коммутационные перенапряжения, приложенные к обмотке статора, носят импульсный характер. Способность изоляции противостоять импульсным перенапряжениям характеризуют коэффициентом импульсной прочности *HMn=HMn/(V2t/) , гдс Г - среднес

пробивное напряжение при частоте 50 Гц; г/имп -то же, при импульсном напряжении. Результаты проведенных исследований показывают, что импульсное напряжение более опасно, чем напряжение промышленной частоты. Для эмаль-проводов Лимп с увеличением наработки уменьшается, для стекловолокнистой изоляции - увеличивается.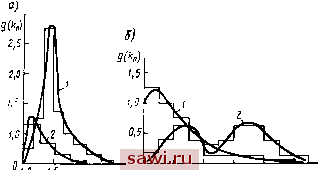

2,0 2,5 к 1,0 1,5

Рис. 11.5. Кривые плотности распределении кратности коммутационных перенапряжений:

а - при отключении электродвигателей, б - прн включении; / - на холостом ходу, 2 - при заторможенном роторе

Напряжение Un, приложенное к секции обмотки статора, определяется величиной фазного напряжения, коммутационными перенапряжениями и взаимным расположением проводников в секции и пазу статора. Коммутационные перенапряжения зависят от многих факторов: вида коммутации (включение, отключение, реверс), волновых параметров обмотки двигателя, типа коммутационного аппарата и др. Поэтому кратность коммутационных перенапряжений имеет случайный характер и может быть в 10 раз больше номинального напряжения. В математическую модель расчета надежности изоляции обмоток электрических машин коммутационные перенапряжения вводятся в виде плотности распределения или в виде фиксированных уровней напряжения. Кратность коммутационных

перенапряжений * = ;7 /(К2/ф) , где LmK -амплитуда коммутационного перенапряжения; L/ф--номинальное фазное напряжение двигателя. На рис. 11.5 приведены в качестве примера кривые плотности распределения кратностей коммутационных перенапряжений g(kn) относительно корпуса для одного из серийных двигателей мощностью до 100 кВт. На основе статистической обработки большого числа осциллограмм, снятых при исследовании ряда асинхронных двигателей, была получена обобщенная кривая плотности распределения кратностей коммутационных перенапряжений, приведенная на рис. 11.6. Эту кривую можно аппроксимировать

суперпозицией двух законов распределения: усеченного нормального с математическим ожиданием ka=\ и усеченного распределения Коши с модой Лп=3. При этом

gikj = exp[ {К - 1 )V0,08J + 0.35/[ 1 + - Щ. (11.15)

Напряжение Uu, воздействующее на элементы витковой изоляции обмотки статора, зависит также от распределения коммутационных перенапряжений по длине обмотки (по секциям и виткам), а для всыпных обмоток и от распределения проводников в пазу. В результате проведенных экспериментальных исследований было установлено, что в асинхронных двигателях напряжением до 1000 В длительность переднего фронта коммутационных перенапряжений обычно составляет Ф7 МКС и что при такой длительности максимальные напряжения распределяются равномерно по секциям и виткам. Однако перемешивание проводников при укладке их в пазы увеличивает напряжение между парами соседних проводников, что обусловливает неравномерность распределения напряжений по отдельным виткам. Экспериментальная проверка расположения проводников всыпной обмотки в полузакрытых пазах на двигателях различных типоразмеров показала, что вероятность распределения проводников в пазу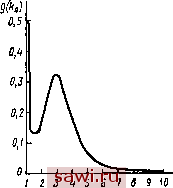

Рис. 11.6. Кривая плотности распределении кратности коммутационных перенапряжений

P{l,) = \n{wJl,)l{Q,Q%w~ 1,6),

(11.16)

где Wc - количество проводников в секции; - порядковый номер проводника в соответствии с последовательностью их намотки на шаблон (рис. 11.7). На рис. 11.8 изображены кривые 2, 3, и 4 распределения вероятности Я( ), полученные из опыта для секций с 18, 32 и 72 витками и теоретические кривые /, построенные по уравнению (11.16). Сравнение кривых / с кривыми 2, 3, и 4 подтверждает хорошее совпадение формулы (11.16) с экспериментальными результатами. При этом установлено, что вследствие перемешивания проводников при всыпании их в полузакрытый паз напряжение между ними составляет в среднем 25% напряжения, приложенного ко всей секции, это снижает надежность всыпной обмотки по сравнению с обмоткой, у которой проводники секции расположены в пазу упорядоченно.

Таким образом, распределение приложенных напряжений между соседними витками с учетом распределения проводников в пазу

а вероятность безотказной работы

g(fen).

г- и.

Lf/b/*n

(11.17)

(11.18)

Согласно рассмотренной математической модели надежность витковой изоляции определяют по следующей методике: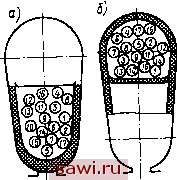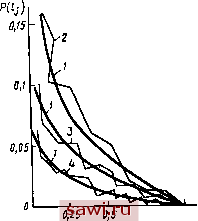

0,75 ио Ij

Рис. 11.8. Кривые вероитиости распределении проводников в пазу при всыпной обмотке

Рис. 11.7. Распределение проводников в пазу при двухслойной обмотке:

а - сторона катушки, уложенная в верхний слой, б -сторона катушки, уложенная в нижний слой; /... - номера проводников

1. Определяют количество элементов п модели по формуле, полученной из расчета среднего числа проводников, с которыми соприкасается каждый проводник в пазу

где - число эффективных проводников в обмотке; Wc - число эффективных проводников в секции; с -число сторон секции в пазу (для однослойной обмотки с=1, для двухслойной с=2); 2 -число пазов.