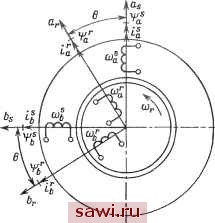Рис. 1.7. Модель двухфазной машины в не-преобразованной системе координат

машины были предложены Г. Кроном в 30-х годах, и в последние десятилетия теория обобщенной машины получила дальнейшее развитие в работах советских и зарубежных ученых [13].

Дифференциальные уравнения, описывающие переходные и установившиеся процессы в обобщенной машине в естественных или фазовых непреобразованных координатах (рис. 1.7), имеют вид

ui = ilrl + dlldt; -ua = iy, + d4 a/dt; -ub = i-brb + drb/dt.

В (1.3) потокосцепления обмоток Чо = Lim, + М (cos 6)+ М (sin 6) 1ь; 4-1 = Ш1 + М (cos 6) il - М (sin 6)

= + М (cos 9) il - М (sin 6) %; Vt = Ubib + M (cos 6) il + M (sin 6) Ц.

(1.3)

(1.4)

В (1.3) и (1.4) ul, иъ, Иц, - напряжения на обмотках статора и ротора; io, 1%, io, tb - токи в обмотках статора и ротора; г1, г1, Гд, rfc - активные сопротивления обмоток статора и ротора; L, Д, Д, LJ-индуктивности обмоток статора и ротора; М - взаимная индуктивность между обмотками статора и ротора; 6 - угол между осями обмоток статора и ротора.

Если подставить (1.4) в (1.3), получатся громоздкие уравнения с периодическими коэффициентами. Для упрощения уравнений электромеханического преобразования энергии рассматривается псевдонеподвижная машина, в которой в обмотки ротора вводится ЭДС вращения. При этом в неподвижной и вращающейся машинах токи, активная и реактивные мощности остаются неизменными.

В неподвижной системе координат а, Р уравнения обобщенной машины, выраженные через потокосцепления. выглядят следующим образом:

dt di

d4 , (1-5)

Подставляя в (1.5) значения потокосцеп-лений

4 = LUa + Mi-; 4 = Ii + Mip; 4i = L;;ii + M,l;

(1-6)

получаем выраженные через токи уравнения напряжений для машины, которые удобно записывать в матричной форме:

(1.7)

В (1.5)-(1.7) 4, 4, L ир. р. ip - соответственно напряжения и токи в обмотках статора и ротора по осям а и Р; )- , р, а, р - активные сопротивления обмоток статора и ротора; М - взаимная индуктивность; La, 1, La, ip - полные индуктивности обмоток статора и ротора по осям а и Р; со, - угловая скорость ротора.

Индуктивности обмоток определяются по известным соотношениям

(1.8)

где la, /р, (а, (р - индуктивности рассеяния обмоток статора и ротора по осям а и р.

Активные сопротивления и индуктивности в (1.7) относятся к фазе машины и определяются расчетным и опытным путем.

Применяя преобразования координат при инвариантной мощности, получают уравнения в других координатах [12].

Процессы преобразования энергии в переходных процессах описываются уравнениями напряжений (1.5) или (1.7) и уравнением движения

I , dco,.

(1.9)

р dt - где Мэ - электромагнитный вращающий момент - момент, создаваемый машиной; - момент сопротивления с учетом момента трения; р - число пар полюсов; / - момент инерции.

Вращающий момент

может иметь и другой вид. Вращающий момент можно определить также через намагничивающие токи и через изменение энергии магнитного поля или из выражения вектора Пойнтинга [12, 13].

При круговом поле в воздушном зазоре нарашивание сложности уравнений происходит при учете нелинейностей параметров и учете нескольких контуров на статоре и роторе.

Уравнения электромеханического преобразования энергии усложняются при наличии двух полей в воздушном зазоре машины. При эллиптическом поле система уравнений электромеханического преобразования энергии состоит из восьми уравнений напряжения и уравнения электромагнитного момента с четырьмя парами произведений токов в обмотках статора и ротора. Число уравнений увеличивается при учете контуров с токами на статоре и роторе Учет нескольких полей и контуров на статоре и роторе приводит к системе с несколькими десятками уравнений. Наиболее простая система уравнений - система уравнений третьего порядка - получается, если использовать описание процессов преобразования энергии через обобщенные векторы [13];

dt

- di> dt

(1.14)

Мэ=-M( -;-c/p),

(1.10)

где m - число фаз.

Вращающий момент может быть выражен;

через потокосцепления (1.6):

2 rL-M(P - P

(1.11)

через потокосцепления и токи статора:

М, = - {ЧЩ-Ч1,Ц),

(1.12)

через потокосцепления и токи ротора:

Мэ = -(Ч 1!;-ЧрЙ-

(1.13)

Справедливость (1.11)-(1.13) подтверждается, если в (1.10) подставить значения по-токосцеплений и токов из (1.6). Вращающий момент после преобразований (1.10)-(1.13)

Система уравнений (1.14) и уравнение движения (1.9) описывают динамические и статические характеристики электрической машины.

Уравнения установившегося режима получаются из дифференциальных уравнений путем замены в уравнениях электромеханического преобразования энергии оператора дифференцирования:

d/dt уш.

В установившемся режиме уравнения напряжений и уравнение движения могут рассматриваться независимо друг от друга. Простейшие уравнения в установившемся режиме получаются из схем замещения электрических машин и упрощенных уравнений, на базе которых строятся векторные диаграммы. Математические модели для различных типов электрических машин в установившихся режимах весьма разнообразны и описаны подробно в [5, 10, 12].

Круговое поле в воздушном зазоре мо-

жет быть только в идеализированной машине. В воздушном зазоре реальной электрической машины имеется бесконечный произвольный спектр гармоник поля, состояший из временных и пространственных гармоник. Высшие гармоники в воздушном зазоре машины появляются за счет несинусоидальности напряжений, несинусоидального распределения МДС, неравномерности зазора, насыщения и других причин.

Наиболее общей математической моделью, позволяющей записать уравнения для бесконечного спектра гармоник и любого числа контуров на статоре и роторе, является модель обобщенного электромеханического преобразователя - двухфазной электрической машины с т обмотками на статоре и и обмотками на роторе (рис. 1.8).

Модель обобщенного электромеханического преобразователя дает возможность записать уравнения при наличии высших гармоник в воздушном зазоре и нескольких контуров на статоре и роторе.

Для обобщенного электромеханического преобразователя записываются уравнения в матричной форме:

U = ZI; Мэ = М1Т. (1.15)

В (1.15) входят столбцовые субматрицы напряжений и токов с т, п числом напряжений и токов. В матрицу сопротивлений Z входят 12 сложных субматриц сопротивлений [12, 13].

Электромагнитный момент определяет-

Ifi 2fi 0-? nf

\nrxt-rpr

It 4?

ся произведениями всех токов, протекающих в обмотках статора и ротора обобщенного электромеханического преобразователя (1.15).

Современные ЭВМ позволяют решать в течение нескольких минут 30- 40 уравнений, составленных на основе модели обобщенного электромеханического преобразователя. Это обеспечивает учет трех-четырех гармоник в воздушном зазоре и двух-трех контуров на статоре и роторе.

При исследовании электрических машин используются также уравнения, составленные на базе уравнений теории поля. Они дают возможность решать многие задачи статики. Однако при решении задач динамики уравнения обобщенного электромеханического преобразователя имеют большие преимущества Развитие теории электрических машин долгое время шло по пути применения отдельно уравнений поля и теории цепей, тогда как наиболее плодотворным является их сочетание в математической модели [13].

Развитие современной теории электромеханического преобразования энергии позволяет составить математическое описание процессов преобразования энергии для любого случая, встречающегося в практике современного электромашиностроения. Квалификация инженера-электромеханика во многом определяется умением упростить математическую модель без потери необходимой точности и возможности решения поставленной задачи в кратчайшие сроки с помощью имеющейся вычислительной техники.

1.4. Параметры электрических машин

Параметры электрических машин - это коэффициенты перед независимыми переменными в уравнениях электромеханического преобразования энергии. Как правило, параметрами являются активные сопротивления, взаимные индуктивности, индуктивности рассеяния и полные индуктивности обмоток. Параметром машины является также момент инерции

Рис. 1.8. Математическая модель обобщенного электромеханического преобразователя