этой кривой криволинейный интеграл

(2.55)

Циркуляция зависит от направления интегрирования, и Г = = -Tab- Если контур С замкнут, то имеем в (2.55)

Тс = оа dr = oai dxi.

(2.56)

При этом положительным считается обход контура С против часовой стрелки.

Если поле а(х1,Х2,хз) потенциально, то по определению (2.55) циркуляция Г равна

Tab =

grad if df =

dip = if

-ip)

(2.57)

Ha плоскости {px\X2) рассмотрим элементарный замкнутый контур С, ограничивающий прямоугольник со сторонами Axi и Ах2 и площадью АНз = AxiAx2 (рис. 18). Так как согласно определению (2.56) dVc = aidxi, то

Гс = АГ = aiAxi + (а2 + Аа2)Ах2 - (ai + Aai)Axi -

Аа2 Аа\

- аАх = Аа2Ах2 - Aai Axi =

Axi Ах2 7

)АЕз. (2.58)

Устремляя стороны Axi и Ах2 к нулю, тем самым стягивая контур С к точке О, получим

дх\ дх2

= (rota) kdT. = (rota) -йз, (2.59) dV

(rota)3 =

(2.60)

T. e. каждая компонента ротора векторного поля есть изменение циркуляции по соответствующему замкнутому контуру на единицу площади, ограничиваемой этим контуром. В этом со-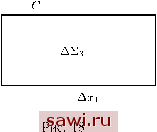

Рис. 19

стоит механический смысл дифференциального оператора rot, определённого с помощью (2.22). Из формулы (2.59) следует

rot а =

rot а ndTi,

(2.61)

Направление нормали в (2.61) выбирается так, что с конца вектора п обход контура С виден в положительном направлении. Соотношение (2.61) называется формулой Стокса О, означающей, что циркуляция векторного поля вдоль замкнутого контура равна потоку (в соответствующем направлении) ротора данного поля через любую поверхность, натянутую на этот контур. Для векторного поля скорости v (2.61) имеет вид

vdr = 2

udY..

(2.62)

Рассмотрим вихревую трубку, ограниченную контурами С\ и (рис. 19). Пусть Сз и С4 - контуры по образующей этой трубки. Обозначим через Ya поверхность, натянутую на С = = Ci и Сз и С2 и С4. Тогда, очевидно.

v df = кроме того,

V df= 2

с, Сз С2 С4

V df= 0.

dS = 0. (2.63)

(2.64)

)Она справедлива для односвязных областей Е.

3 Б.Е. Победря, Д.В. Георгиевский

Vdr. (2.65)

Таким образом, доказана

Первая теорема Гельмгольца. Циркуляция скорости вдоль любого контура, охватывающего одну и ту же вихревую трубку, постоянна.

Эта циркуляция называется напряжённостью вихревой трубки и служит важной её характеристикой:

у. dr. (2.66)

Согласно формуле Стокса (2.62) и первой теореме Гельмгольца величина равна удвоенному потоку (в положительном направлении) вектора вихря и через любое сечение вихревой трубки. Таким образом, данный поток также может служить характеристикой вихревой трубки.

Утверждение, аналогичное первой теореме Гельмгольца, справедливо не только для ш, но и для любого соленоидального поля. Так, например, если поле скоростей v соленоидально, т. е. существует векторный потенциал ф (2.25), то величина iy,

tfdr, (2.67)

постоянна для любого контура С, охватывающего трубку тока, и представляет собой напряжённость трубки тока. Величина iy также равна потоку скорости через любое сечение трубки тока.

Вторая теорема Гельмгольца. Вихревая трубка не может начинаться либо обрываться внутри тела, а должна быть замкнутой либо выходить на границу тела.

Действительно, в силу того что поток вихря через любое сечение вихревой трубки постоянен, модуль вектора и в месте обрыва трубки или стягивания её в одну точку был бы равен бесконечности. В природе замкнутыми вихревыми трубками являются, например, кольца дыма, выходящего из трубы. Водоворот также представляет собой вихревую трубку, один конец

Обозначая через С2 контур С2 с противоположным обходом, получим