которой упирается в дно, а другой выходит на поверхность водоёма. Особо опасен смерч - трубка, обладающая огромной напряжённостью и способная, как известно, вырывать с корнем деревья и переносить тяжёлые предметы на большие расстояния. Один конец такой трубки опирается на землю или поверхность океана, а другой уходит в слой облаков.

Возьмём теперь производную по времени от циркуляции скорости по кривой, соединяющей точки А и В иг рис. 17:

d dt

df =

в в

w dr +

dv =

(2.68)

Если точку в устремить к А, тем самым образуя контур С, то \Щв \Ща, и из (2.68) будем иметь

--(i)v df= ф dt

(2.69)

Равенство (2.69) составляет утверждение кинематической теоремы Кельвина.

Теорема Кельвина. Производная по времени от циркуляции скорости вдоль замкнутого контура равна циркуляции ускорения вдоль того же контура.

Иногда теорему Кельвина формулируют и для разомкнутой кривой в форме (2.68).

ЛЕКЦИЯ 3

ИНВАРИАНТНОСТЬ КИНЕМАТИЧЕСКИХ ВЕЛИЧИН

Место, занимаемое частицей X в отсчётной конфигурации, описывается соотношениями (1.5), которые представим в виде

В актуальной конфигурации место, занимаемое частицей, описывается соотногиениями (1.6), которые теперь представим в виде

г=г(с, е, ел)=жче, е, т. (з.2)

Если материальные координаты и лагранжевы координаты Xq выбраны прямоугольными декартовыми, то расположение индексов (вверху или внизу) у компонент радиусов-векторов го и г не имеет значения:

е = й, х1 = х1 (3.3)

Иначе обстоит дело, если выбранная система координат является криволинейной. Даже если координатные линии, составленные из материальных частиц Xq = const или = const в отсчётной конфигурации были прямолинейными, то в актуальной конфигурации они, вообще говоря, становились кривыми. В некоторых случаях и в недеформированном состоянии бывает удобней вводить ту или иную криволинейную систему координат. Предположим поэтому, что линии =

= const (i = 1, 2, 3), выбранные в некоторой точке (3.1) (рис. 20), таковы, что выполняются условия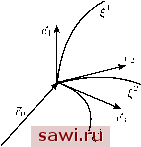

(3.4)

Рис. 20

Тогда тройка векторов dfo

так называемого ковариантного локального базиса отсчётной конфигурации будет некомпланарной.

ei =

(3.5)

\ea\ = Va ea = (3.7)

Обратная к gij матрица g, удовлетворяющая соотношениям

99kj = Sr gjk9 = S/, g=g\ \дЦ = -, (3.8)

называется контравариантной фундаментальной матрицей отсчётной конфигурации.

Путём поднятия индексов у векторов ковариантного локального базиса

е- = 5е, (3.9)

МОЖНО получить контравариантный локальный базис отсчётной конфигурации. Вообще говоря, он не является голоном-ным, т. е. связанным с какой-либо системой координат. Заметим, что

е- . е-- = 5Vefc el = ддды = = д (3.10)

ej = g,ke = дид = 6/. (3.11)

Рассмотрим произвольное векторное поле а в отсчётной конфигурации. В каждой точке вектор а может быть разложен по векторам как базиса (3.5), так и базиса (3.9):

S=aei = aie\ (3.12)

Пусть - новая криволинейная система координат, связанная со старой законом преобразования

е= е{е,е,е)- (злз)

При этом

0. (3.14)

Тогда матрица = д/д будет невырожденной в каждой точке и существует обратная ей матрица В\, = д/д:

А]ВГ, = 5] В,А] = 5у (3.15)

Определим теперь ковариантную фундаментальную матрицу отсчётной конфигурации:

gij = gji = ei ej, g=\gij\0, (3.6)

Согласно (3.5) и (3.6)