Установка Видеонаблюдения, Охранной и Пожарной сигнализации.
Звоните! Приедем быстро! Установим качественно! + гарантия 5 лет.
| Тел. ОАО «Охрана Прогресс» Установка Видеонаблюдения, Охранной и Пожарной сигнализации. Звоните! Приедем быстро! Установим качественно! + гарантия 5 лет. |
||
|
Установка технических средств охраны. Тел. . Звоните! Главная Элементы теории определяющих (факторов) 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 ЛЕКЦИЯ 5 МАЛЫЕ ДЕФОРМАЦИИ Деформации называются малыми, если перемещения малы: гг <С I, где I - диаметр рассматриваемого тела, и все компоненты тензора дисторсии по модулю много меньше единицы: W < 1. (5.1) Согласно (4.20) и (4.17) в этом случае имеем Vn = I- (1 +W)- = = /-(I-W+(W)2-...) W, (5.2) так как слагаемые порядка (УгГ), п 2, в (5.2) имеют в си- лу (5.1) более высокий порядок малости, чем VU. Таким образом, тензоры дисторсии недеформированного и деформированного состояний совпадают: щге®ё Uj\,E®&. (5.3) Поэтому разница между лагранжевым и эйлеровым описанием (лагранжевыми и эйлеровыми координатами) в случае малых деформаций исчезает. Тензоры Лагранжа и Эйлера (4.11), (4.12) в этом случае совпадают: 1 о ° 7 = э = 6 = Eije = - (уй + {Vuy ). (5.4) Компоненты eij тензора малых деформаций е выражаются через перемещения следующим образом: ij = + = (5.5) Соотношения (5.5) называются соотношениями Коши. Вычислим для рассматриваемого случая другие меры деформаций, введённые в прошлой лекции. Согласно определениям (4.22)-(4.25) имеем С = F . = (/+ W) (/+ W) l + VU+ (Vuf = / + 2б, (5.6) B = F -¥={1 + Vuf {L + Vu) ~ / + (W) + V = / + 2e, (5.7) 4 = F F = (X - Vn) (/ - Vn) / - W- (W) = L-2e, (5.8) M = F-- F- = U- W) (I - W) X - [Vuf - W = I - 2e. (5.9) Разложим тензор дисторсии Vu на симметричную и антисимметричную части: о УгГ=б + 0, (5.10) так что симметричный тензор деформаций е связан с и соотношениями (5.4), а антисимметричный тензор поворотов Q и его компоненты имеют вид О = (W- (W)), О = -{щ - u j) = [,-,]. (5.11) С тензором поворотов естественным образом свяжем вектор поворотов О: И аналогично (4.60), (4.61) найдём О = 2л/СбыО 0. (5.13) Выражения для левого и правого тензоров растяжения и тензора враш,ения примут вид И = С1/2 = л/7Т2/ + б, (5.14) @ = И £=(/-£) а + £+0)1 +О, (5.15) U = Q-F={L-Q)U + e + Q)L + e. (5.16) Выясним геометрический смысл компонент sij тензора малых деформаций. Рассмотрим для простоты в недеформированном состоянии ортонормированный базис fc, так что gij = 5ij и = 1. Выберем в этом состоянии материальное волокно dr й = -enjEk = eVгUJЁk = rot и, (5.12) в направлении оси с номером а {координатное волокно): dXa > 0. (5.17) Если локальным базисом деформированного состояния является базис Ei, то это же координатное волокно описывается теперь вектором df\ dr =dXaEa. (5.18) Заметим, что согласно (4.1) в данном случае Gaa=+£aa и Ga(3 = 2бск/5. Найдём отношение Iq, длин (3.57): 1(У - / dxq-Eq dxqEJq dx (ylxiQ dx (ylxiQ Таким образом, aa - la ~ - l+e . (5.19) (5.20) T. e. каждая диагональная компонента ea представляет собой относительное удлинение координатного волокна, направленного по оси а. В этом состоит геометрический смысл диагональных компонент тензора малых деформаций. Вычислим теперь угол ipoLJ между координатными волокнами df() и df (). Из (3.60) имеем () . df (/?) -=dfHdf(/) dxoEo, dxE dxaEa dxaEa\/dxpEp dxpEp 2sap. (5.21) л/1+2б1+2бда Ho COS (pa(3 = sin(7r/2 - (fap) 7г/2 - (fap = /j a(3, ибо угол (/9 между координатными волокнами dfg и drj прямой. Итак, недиагональная компонента равна половине угла скашивания 7г/2 - (ра(з ИЛИ половине разности углов между соответствующими координатными волокнами (рис. 21). В этом заключается геометрический смысл компонент тензора деформаций со смешанными индексами. Наконец, найдём отношение элементарных объёмов dV и dVo в данной Рис. 21 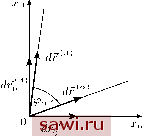 Установим охранное оборудование. Тел. . Звоните! |