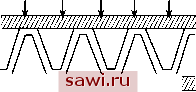Рис. 2

Отметим, что принцип континуализации, используемый для введения сплошной среды, не решает всех проблем. После постановки задачи МСС требуется привлечение вычислительной техники для её решения. Для этого задачу требуется превратить в алгебраическую, т.е. провести процесс дискретизации. В целях анализа полученного решения и сравнения его с экспериментальными результатами приходится вновь континуализировать задачу.

Таким образом, процессы дискретизации и континуализации задачи МСС повторяются несколько раз на различных уровнях. Частично такими проблемами занимается бурно развивающийся раздел механики - вычислительная механика [42]. Об этом пойдёт речь в дальнейшем.

Для описания событий, происходящих в сплошной среде, выберем некоторую систему отсчёта. Чаще всего это будет инер-циальная система отсчёта: х О. Одномерное пространство называется временным: О < t < ос, а пространство О - координатным. Инерциальной системой отсчёта она называется потому, что в ней справедлив закон инерции, т. е. она либо покоится, либо движется относительно другой инерциальной системы поступательно, равномерно и прямолинейно. Геометрические свойства и размерность пространства О выбираются в зависимости от цели предпринимаемого исследования.

Предположим, что существуют двумерные создания, живущие в плоскости листа (рис. 1). Чтобы сделать операцию на сердце такому созданию, двумерный хирург должен сначала рассечь тело пациента. Мы же, трёхмерные люди, можем коснуться его сердца, не производя никаких разрезов. Если такие двумерные создания живут на гофрированной двумерной поверхности, которую сжали с обеих сторон двумя жёсткими плитами, то они будут испытывать напряжённое состояние , от которого нельзя освободиться никакими силами, действующими

в ПЛОСКОСТИ деформированного гофра (рис. 2). Ведь гофр может разгрузиться только в трёхмерном пространстве, которое для двумерных созданий является математической абстракцией.

Точно так же в нагаем реальном трёхмерном мире возникают напряжения (например, при сварке), от которых можно освободиться только выходя, вообще говоря, в гаестимерное евклидово пространство. Поэтому, чтобы изучать такое напряжённое состояние, нужно в качестве О рассматривать гаестимерное евклидово пространство или трёхмерное риманово пространство [38, 39].

Однако чаще всего за координатное пространство О принимается трёхмерное евклидово пространство М , которое будем также называть вмещающим ящиком Я. В нём всегда может быть введена прямоугольная декартова система координат, благодаря чему любая точка вмещающего ящика Я описывается радиусом-вектором f=Xiki, где kj - векторы ортонормирован-ного базиса О . Величины Xi называются пространственными координатами данной точки или данного места в ящике Я.

Определим далее тело В (сплошную среду) как трёхмерное дифференцируемое многообразие. Под многообразием понимается множество Е, представленное в виде объединения {Щ конечного или счётного числа областей. Для каждой области U задано взаимно однозначное отображение её в открытую область трёхмерного евклидова пространства Ш? (задан гомеоморфизм в Ш?). Тем самым в каждой области заданы координаты i,23 {U - координатная окрестность или карта; совокупность карт называется атласом). Пересечение U r\U каждой пары областей в каждом множестве Е является областью, в которой действуют две системы координат: i,23 (в U) и l2з (в U). При этом одна система координат выражается через другую соотношениями

= (6,6,6). =1,2,3. (1.1)

Функции [ непрерывно дифференцируемы достаточное число раз. Кроме того, во всех точках якобиан преобразования (1.1) отличен от нуля:

/О, (1.2)

о По повторяющемуся индексу г производится суммирование от 1 до 3 (см. стр. 11).

т. е. преобразование -> [ невырожденно или локально обратимо. Тогда по теореме о неявной функции существует обратное к (1.1) преобразование

. = .(;,2з) г =1,2,3. (1.3)

Таким образом, с каждым телом В можно связать атлас (в двумерном случае сфера состоит из двух карт). Если же тело В само является евклидовым пространством или его частью, то атлас состоит из одной карты и может рассматриваться одна система координат для всех окрестностей U - элементов многообразия В .

Элементы тела В называются частицами X, а величины {i = 1, 2, 3) - материальными координатами этих частиц. Конфигурацией Е тела В назовём гладкий гомеоморфизм В в область трёхмерного евклидова пространства R. Таким образом, название частиц связано с одной из таких конфигураций. Движением тела В будем называть однопараметрическое семейство конфигураций E{t) с временным параметром t. Это означает, что в каждый момент времени t имеется фотография тела В в ящике Я.

Итак, конфигурация тела В в момент времени t представляет собой множество всех мест х, которые занимают составляющие это тело частицы X: х = E{B,t) = {Е{Х,t), ХеВ}. Предполагается, что отображение В -> S(i5, t) биективно, т. е. две различные частицы в одно и то же время не могут находиться в одном месте ящика и, наоборот, никакая частица ни в один момент врмени не может занимать два различных места. Это положение носит название гипотезы непроницаемости.

Конфигурация в момент времени t = to называется отсчётной конфигурацией: xo = E{B,to), а в текущий момент t - актуальной конфигурацией: х = E{B,t). Координаты ящика ХрХ2,Хз, соответствующие отсчётной конфигурации, называются лагранжевыми координатами. Они могут, как и материальные координаты, служить наименованием частицы X (её названием ). В отличие от материальных координат 1,2.3. лагранжевы координаты связаны с выбором параметра t = Iq. Поэтому может быть установлено непрерывное и взаимно однозначное соответствие:

x = x(xo,t). (1.4)