Установка Видеонаблюдения, Охранной и Пожарной сигнализации.
Звоните! Приедем быстро! Установим качественно! + гарантия 5 лет.
| Тел. ОАО «Охрана Прогресс» Установка Видеонаблюдения, Охранной и Пожарной сигнализации. Звоните! Приедем быстро! Установим качественно! + гарантия 5 лет. |
||
|
Установка технических средств охраны. Тел. . Звоните! Главная Элементы теории определяющих (факторов) 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 где величина VolI пропорциональна стехиометрическому коэффициенту, с которым компонент а входит в 1-ю химическую реакцию; J/ - скорости химических реакций. Таким образом, + div(p,,) = T,. (6.26) Суммируя п равенств (6.26), придём к уравнению неразрывности (6.11), т.е. сумма образований всех веществ в многофазной среде равна нулю: п п т а=\ а=\1=\ Соотногаения (6.26) представляют собой уравнения неразрывности для каждого компонента многофазной среды. Пользуясь уравнениями неразрывности для многофазных сред, выведем уравнения диффузии p + divi = T , а=\,...,п. (6.28) Для этого преобразуем левую часть (6.26): д р д р + div {paVa) = + div {paVa paV + PaV) f I dp . л дра 1 1 p dt 1 dp . dpoL , dp + pcdiv - Cc,- - padiv - ~~dt d{Cap) dp - dCa , 1. on\ = --c.- + div,. = p-+ div,.. (6.29) Отсюда и следует (6.28). Вернёмся к понятию силы и рассмотрим элемент массы Am, заключённый в объёме AV и содержащий точку М (рис. 24), а также суммарную силу AR, действующую J на этот элемент. Выполняя предельный пе-( ш реход AV lim -- = Рш, (6.30) АУо Am Рис. 24 Д получим новый вектор - массовую силу Р\м, приложенную в точке М. Поле F{x,t) образует векторное поле массовых сил в М и по размерности совпадает с ускорением ( сила, отнесенная к единице массы ). Характерным примером массовых сил является ускорение сил тяготения, в частности ускорение д силы тяжести. Наряду с массовыми силами будем рассматривать объёмные силы X: X = pF. (6.31) Мысленно рассечём плоскостью тело, занимающее объём V (рис. 25) и находящееся в равновесии. Удалим одну из частей этого тела, например правую. Чтобы левая часть оставалась в равновесии, очевидно, к плоскости сечения нужно приложить  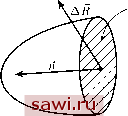 Рис. 25 Рис. 26 некоторые силы (рис. 26). Выделим на этой плоскости элементарную площадку АН и обозначим через АД силу, действующую на неё. Стягивая площадку АН к точке М, получим 1 л АЕО AS Вектор 51 называется поверхностной силой в точке М на площадке с нормалью п и имеет размерность давления ( сила на единицу площади ). Величина S\x,t) не образует векторного поля, так как зависит не только от точки пространства, но и от площадки, проходящей через эту точку. На последний факт указывает верхний индекс (п). Для того чтобы найти суммарную силу, действующую на объём V, необходимо проинтегрировать по V вектор X{x,t), а для нахождения суммарной силы, действующей на поверхность И, надо проинтегрировать по S вектор S\x,t). В последнем случае в каждой точке S надо выбирать единичную нормаль n{x,t), отложенную в положительном направлении. Заметим, что SW(f,t) = -S(-)(f,t). Пусть V - произвольный жидкий объём внутри данного тела, а S - поверхность, ограничивающая этот объём. Назовём интеграл pvdV (6.33) количеством движения, заключённым в объёме V. Сформулируем теперь второй постулат механики сплоганой среды, или закон об изменении количества движения. Закон об изменении количества движения (II постулат МСС). Пусть О G М - объём, занимаемый телом в актуальной конфигурации, V - произвольный жидкий объём в а - его граница с единичной внешней нормалью N. Тогда в любой момент времени pFdV + (6.34) т. е. производная по времени от количества движения среды, заключённой в V, равна сумме объёмных сил, приложенных к V, и поверхностных сил, действуюших на S. Интегральная формулировка (6.34) - обобщение второго закона Ньютона на сплошные среды. По лемме 1 (6.18) dQ d ~Jt pvdV = (6.35) Рассмотрим тетраэдр, построенный на векторах A = aEi, В = ЬЕ2 я С = cEs, которые направлены вдоль базисных векторов в деформированном состоянии (рис. 27). Объём данного тетраэдра равен одной шестой объёма косоугольного параллелепипеда, построенного на А, В и С, или, согласно (3.55), V, = = VGabc\ (6.36) о о Обозначим Si, Ti2, Из и S площади треугольников ОВС, ОСА, ОАВ и ABC. Первые три 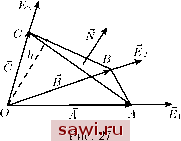 Установим охранное оборудование. Тел. . Звоните! |