И антисимметричной части - спин-тензора R = rije

(X) е->

с компонентами

1 ,°

= o(V.г;,-Vя.)

(7.48)

Наряду с (7.45) имеем ещё одну форму записи величины а:

6а) = -dt

pUj dVo - dt pnj dVo, (7.49)

Причём из-за несимметричности тензора Пиолы второй интеграл в правой части (7.49), вообще говоря, не равен нулю.

ЛЕКЦИЯ 8 НАПРЯЖЁННОЕ СОСТОЯНИЕ В ТОЧКЕ

Рассмотрим тензор напряжений Коши Р и его представление (6.55) в актуальной конфигурации. Изучение будем вести в прямоугольной декартовой системе координат с базисными векторами ki, поэтому все индексы будем писать внизу. Согласно (6.48) вектор истинных напряжений

5W = 5f)fc, (8.1)

на плош,адке с единичной нормалью (рис. 28) представляется в виде

= NjPj = NjPjih. (8.2)

Из (8.1) и (8.2) следует, что компоненты вектора S на любой площадке связаны с компонентами нормали к этой площадке

тензорным законом:

5Р) = Р ЛГ, = Д,ЛГ,. (8.3) На координатных площадках,

где 7V() = ка, ЛГ() = даг, ИЗ

(8.3) имеем

5f = Раг. (8.4)

Таким образом, компонентам тензора напряжений Коши можно придать следующий физический смысл: величина Pji (равная Pij в силу закона парности касательных напряжений (7.7)) в данной точке равна i-u компоненте вектора истинных напряжений, действующего на площадке, проведённой через эту точку, с нормалью в направлении оси с ортом kj. Напряжённое состояние в точке полностью определяется тензором напряжений Р в этой точке [31,61]. Компоненты Раа будем называть растягивающими, а Ра(з - сдвигающими.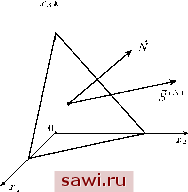

Рис. 28

= JPгJPгkNJNk - {PгJNJN,Y 0. (8.6)

Возвращаясь к координатным площадкам с нормалями N\ из (8.4) и определений (8.5), (8.6) имеем

О -о гьа - -aai

(а) s(a)gia) = рр р2 = р2 + р2.

(8.7)

Исследуем теперь экстремальность величин а и т в фиксированной точке на различных площадках. Существуют ли площадки, на которых касательное напряжение принимает своё минимальное, т. е. нулевое, значение? На таких площадках

вектор S() должен быть параллелен нормали N. Запишем это требование в компонентах:

PijNj = aNi, или {Pij-a6ij)Nj = 0. (8.8)

Система трёх однородных уравнениий (8.8) будет иметь нетривиальное решение лишь в том случае, когда её определитель равен нулю. Это равносильно тому, что а является решением характеристического (векового) уравнения третьей степени

-/12 +/за-/з = 0. (8.9)

Здесь /i, /2, /3 - инварианты тензора напряжений Коши Р:

/i=trP, /2 = trP*, /3 = detP, (8.10)

где Р* - алгебраическое дополнение Р.

Нормальным напряжением а

на площадке с нормалью N назовём проекцию вектора истинных напряжений на N (рис. 29):

5) Рис. 29

Нормальное напряжение представляет

собой квадратичную форму, построенную с помощью симметричной матрицы Pij на компонентах Л-

Касательным напряжением т на площадке с нормалью

назовём проекцию вектора S на саму площадку (или на касательную к площадке плоскость). По теореме Пифагора