R = Cn[- . (11.25)

\ Р J

Чтобы найти константы C\,C2,Cs, достаточно осуществить по одному взрыву каждого из трёх типов. Зная Е и р, надо измерить время t*, за которое фронт волны пройдёт расстоя-

плотность р атмосферы, в которой произведён взрыв, а также характеризующий мощность заряда параметр Е. Последний в зависимости от случаев а, б, в представляет собой либо энергию, либо её линейную или поверхностную плотности соответственно. Таким образом, к = 3, Xi = t, Х2 = р, = Е и

R = f{t,p,E). (11.22)

Размерности всех параметров задачи следующие: [t] = Г, [p]=ML-\ [E]=ML-T-, [R\=L, где Л=1,2,3 для плоского, осесимметричного и точечного взрывов соответственно. Нетрудно заметить, что для любого тройка величин t, р, Е размерно независима, и её можно выбрать в качестве базиса (т = 3).

Для выражения в этом базисе размерности [R] найдём параметры а\, а2 я оз следующей степенной функции:

[R] = [tf[pf2[Ef3 (11.23)

Приравнивая в обеих частях равенства (11.23) показатели при М, L я Т, придём к системе уравнений:

0 = 2 + <з.

1 = -3a2 + {N-l)as, О = а\ - 23.

Её решение таково: a\=2/{2 + N), a2 = -l/{2 + N), 3 = = 1/(2+ Л). Таким образом.

Единственная безразмерная величина в данной задаче имеет вид

Так как fc-m = 3- 3 = 0, то согласно П-теореме П = Ф, причём Ф ни от чего не зависит и равно некоторой константе С. Из (11.24) получим следующее выражение для R:

ние i?* между зарядом и улавливающим прибором. Тогда из формулы (11.25) получим

Скорость V распространения фронта получается дифференцированием по t обеих частей (11.25):

/ Е \ 2+iV

Как видно, г ос при t О, но характер особенности v зависит от Л, т. е. от формы заряда. Интересно, что для увеличения скорости v вдвое в плоском случае надо выбрать заряд в 8 раз мощнее, в осесимметричном - в 16 раз, а в сферически симметричном - в 32 раза!

Подробнее о задаче о сильном взрыве читатель может узнать из книги [51], где также опубликованы фотографии взрыва атомной бомбы в Нью-Мехико в 1945 г. Стробоскопический анализ этих фотографий очень хорошо подтверждает формулу (11.25) для случая Л = 3. По расчётам Дж. Тейлора в момент изображённого взрыва выделилась энергия порядка 10кг-м/с, или 10 МДж. К таким же выводам независимо пришли Л.И. Седов и Дж. фон Нейман.

Задача об обтекании шара потоком. Поместим в горизонтальный поток сжимаемого вязкого газа абсолютно твёрдый шар и будем удерживать его в состоянии покоя. После того, как течение установится, со стороны окружающей среды на шар

будет действовать некоторая постоянная сила F. Следовательно, для удержания его в покое надо приложить силу -F (рис. 41). Величина F = F может за-р висеть от радиуса шара а (ха-

рактерного линейного размера), скорости V газа на бесконечности (характерной скорости) и физико-механических свойств - плотности р, динамической вязкости р и скорости звука с в газе. Таким образом,

F = f{a,v,p,p,c), к = 5. (11.28)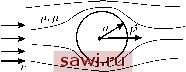

(11.29)

и получающиеся после приравнивания показателей при М, l и Г в каждом из равенств (11.29) три неоднородные системы линейных уравнений:

1=3, ГО = 73,

-l=Pi+p2- < 1 = 71 + 72 - З73,

- 1 = -2, I - 1 = -72,

1 = 3,

\ = ai + а2 - 33, -2 = -а2,

имеющие решения: = 2 = /з = 1, 7i = 7з = О, 72 = 1, <i = = 2 = 2, оз = 1-

Итак, в задаче образуются три безразмерных критерия:

avp V avp

Величины, обратные П1 и П2, в механике сплошной среды носят название чисел Рейнолъдса (Re) и Маха (М). Если М< 1, то имеем дозвуковой поток газа, а если М > 1, то сверхзвуковой. Согласно П-теореме

f = pva4{Ui,U2) = pV(Re,M). (11.30)

Таким образом, безразмерная сила П зависит только от двух параметров (fc - т = 5 - 3 = 2): Re и М. Если эффектом сжимаемости набегающего потока можно пренебречь (тогда речь идёт о вязкой несжимаемой жидкости), то у функции остаётся один

Выпишем размерности определяющих параметров и определяемой величины: [a]=L, [v]=lt~, [p]=ml~, М = = ml-t-\ [с] = lt-\ [f] = mlt-. Любые три из первых четырёх определяющих параметров размерно независимы. Результат не должен зависеть от того, какую тройку величин включить в базис, поэтому положим: х\ = а, Х2 = v, Х3 = р, Х4 = р, Х5 = с.

Для выражения размерностей [р], [с] и [f] в базисе a,v,p запишем три степенные функции:

= [а]А [vf[pf\ [с] = [аР [vW, [f] = [af [уГЧр\