Установка Видеонаблюдения, Охранной и Пожарной сигнализации.
Звоните! Приедем быстро! Установим качественно! + гарантия 5 лет.
| Тел. ОАО «Охрана Прогресс» Установка Видеонаблюдения, Охранной и Пожарной сигнализации. Звоните! Приедем быстро! Установим качественно! + гарантия 5 лет. |
||
|
Установка технических средств охраны. Тел. . Звоните! Главная Элементы теории определяющих (факторов) 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 если такой процесс начинается и заканчивается при одинаковых значениях параметра состояния, то он называется термодинамическим циклом. Большое значение имеет деление термодинамических процессов на обратимые и необратимые [14]. Обратимые могут протекать в любом направлении (значение параметров состояния остаётся прежним при замене t на -t). Необратимые процессы протекают только в одном направлении и описывают выравнивание температуры, давления и т. п. В механике очень часто приходится иметь дело с неизотермическими процессами, т. е. с изменяемой со временем температурой, которая всегда считается термодинамическим параметром состояния. Для изучения таких процессов придётся рассмотреть основные законы феноменологической термодинамики. Будем считать, что понятие температуры интуитивно известно каждому читателю. Введём (также без строгого определения) понятие теплоты Q. Первый закон термодинамики (он имеет много формулировок) утверждает, что теплота есть вид энергии. На основе закона сохранения энергии полная энергия будет состоять из суммы механической и тепловой энергий. Механическая энергия в статике упругого тела описывается потенциальной энергией деформации (10.42): = -Л . (12.3) Тогда полная энергия Е для неизотермического процесса должна иметь вид Е = (f + Q = const. (12.4) Если же для рассматриваемой модели изменение работы внутренних сил не может выражаться полным дифференциалом, как это имеет место для упругой модели (10.41), то закон сохранения энергии естественно представить в дифференциальной форме dE = -dA +6Q, (12.5) где Е называется внутренней энергией, которая зависит от температуры Г и других термодинамических параметров состояния (например, от некоторых тензоров pi, i= 1,2,...). Внутренняя энергия есть работа, которую надо совершить, чтобы перевести систему из одного состояния Т\ pf в другое Г pf\ Периодически действующее устройство для превращения тепла в работу - тепловая машина - может работать только при наличии различных температур Г и Г. С её помощью можно создать термодинамический цикл. Тогда из (12.5) следует, что Р г г odE = 0, обЛ =o6Q, (12.6) или ... = д. (12.7) Отсюда следует ещё одна формулировка первого закона термодинамики: невозможно создать вечный двигатель первого рода - машину, которая могла бы совершить механическую работу, не затрачивая энергии. Ещё одна формулировка первого закона термодинамики, говорящая об эквивиалентности тепла работе, следует из размерности величины Q: [Q] = 1 кал 4,186 Дж, (12.8) причём 10~Дж = 1 эрг = 1 см г/с. Калория, джоуль и эрг служат для измерения Q. Для того чтобы более чётко проследить действие законов термодинамики на конкретной модели, выберем в качестве таковой модель совершенного газа [4,62]. Для него определяющее соотношение записывается в виде уравнения состояния Клапейрона p = pRT, (12.9) где R - газовая постоянная, которая для воздуха равна i? 287,042 м/(с град). Иногда вместо величины R вводят другие постоянные, следующие из соотношений i?= = -, (12.10) Mo mo где Mo - средняя масса одной грамм-молекулы газа, шо - средняя масса молекулы в граммах, Rq 8,314 Юэрг/(моль х X град), fco 1,38 10~эрг/град - постоянная Больцмана. Тогда уравнение состояния (12.9) записывается в одной из двух следующих форм: pV = RoT (12.11) pv = kT, (12.12) V=, v=, v=l, 7V= = 6,023. 101 (12.13) p p N mo Число называется числом Авогадро. Используя последнее из соотношений (12.2) и принимая объём, по которому происходит интегрирование, конечным, но настолько малым, что внутри него величины р и р неизменны, получим =ppVd-. (12.14) Учитывая первое соотношение (12.13), из которого следует, что Md-dV, Р (12.15) Ti < Т2 < Тз имеем для совершенного газа =pdV. (12.16) Тогда из формулировки (12.5) первого закона термодинамики получим SQ = dE + pdV. (12.17) Нам будет удобнее пользоваться уравнением состояния совершенного газа в форме (12.11). Из (12.11) следует, что изотермы описываются уравнением (рис. 42) рУ = const. (12.18) Можно ввести шкалу температур совершенного газа, полагая температуру равной pV/Ro вдоль изотермы одного моля такого газа. Однако в дальнейшем при формулировке второго закона термодинамики будет ясно, что понятие температуры не должно зависеть от свойств среды. Теплоёмкость с системы равна количеству тепла AQ, которое нужно подвести к системе, чтобы повысить её температуру на АГ при заданных условиях: с= lim (12.19) Если при этом поддерживается постоянный объём, то из (12.17) имеем 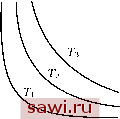 Рис. 42 (12.20) Установим охранное оборудование. Тел. . Звоните! |