F(W = lim-

to+r

F{q{t),p{t), t)dt (16.39)

Если F не зависит от to е [0;Го], то говорят, что система при t <Tq находится в равновесном состоянии. Множество равновесных состояний системы при фиксированных внешних макроскопических условиях носит название равновесного ансамбля этой системы.

Статистическая механика применительно к МСС оперирует средними значениями детерминированных функций [15]. В статистически однородных системах для любой функции F

{F) = F, (16.40)

Т.е. среднее по ансамблю совпадает со средним по времени. В этом заключается известная в теории вероятностей гипотеза эргодичности. В рамках данной гипотезы все средние значения разумно трактовать как макроскопические параметры, которые можно измерить в экспериментах.

Образуем формально из ЗЛ обобщённых координат q векторы gi,..., с компонентами

Ч\ = {ч\Ч2.Чъ) iv = (3iv-23iv-i3iv) (16.41)

и назовём условной вероятностью функции F{q,p,t) величину

F(f, t) = F{q, p,t)f{qu q-s 3a+b p) dq dp,

J (16.42)

a= 1,...,Л.

В (16.42) в числе аргументов плотности вероятности отсутствуют компоненты вектора qa при некотором а, т. е. точка qa зафиксирована.

Оно зависит лишь от времени. Так, среднее по ансамблю от функции Гамильтона есть полная энергия системы:

МН = Е. (16.37)

Дисперсией F{q,p,t), или моментом второго порядка F{q,p,t), называется величина

DF = M(F - MFf = {{F - {F)f). (16.38)

Можно определить и другие средние значения F, например среднее по времени

Оперирование с условными вероятностями и средними величинами сильно упрощается с помощью аппарата 5-функций Дирака, о которых уже упоминалось в лекции 2. Основное свойство 5-функции, которое можно принять в качестве её определения, заключается в том, что для любой непрерывной на отрезке [а; Ь]

функции Lp{x) ь

WW /() я а<х<Ь, \ у)\у) ~ ] о, если X < а или хЪ.

Из (16.43) следует, что

;i6.43)

8{х -y)dy =

6(у) dy =

1, если а < X < b, О, если X < а или х Ь,

5{y)dy=\, 5{-х) = 5{х)

;i6.44)

h{x) =

;i6.45)

для любого положительного числа е.

Кроме того, вводя в рассмотрение функцию Хевисайда h{x), или ступенъку\

1, если X О, О, если X < О,

запишем символьную связь 5{х) и h{x)\

5{x) = h\x). (16.46)

Для проведения стандартных операций математического анализа разрывные функции 5{х) и h{x) можно аппроксимировать последовательностями непрерывных 5-образных (рис. 49)

hi{x)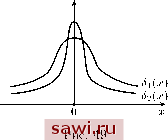

и /i-образных (рис. 50) функций. При этом 5-образные функции 5а выглядят следующим образом:

\1ш8а{х) = 8{х), (16.47)

fx) dx

где ф{х) О - произвольная интегрируемая на всей оси функция. Такими функциями могут быть, например,

ф,{х) = е--\ ф{х) = -, т\. (16.48)

1 ~~ X

в качестве же /i-образных функций ha{x) проще всего взять первообразные функций (16.48).

Продифференцируем по х соотношение (16.43) и воспользуемся формулой интегрирования по частям:

f д

5{х - у)(р(у) dy = -

5{х - y)ip{y) dy =

= -S(x - b)(p(b) + 5{x - a)(p(a) +

5{x-y)ip{y)dy. (16.49)

Так как 5{x - a) = 5{x - Ь) = О во всех точках интервала а < < X < Ь, то из (16.49) получим

6{х-у)р\у) dy.

(16.50)

Рассмотрим также многомерные 5(г)-функции, понимаемые как 6{г) = 5{хх)5{х2Щхъ), (16.51)

ИЛИ, для векторов (16.41):

КЧа) = S{q3a-2)S{q3a-r)S{q3a). (16.52)