Для магнитного поля не существует других зарядов, кроме свободных, и

AivHdV =

div (Б - АтгМ) dV =

div MdV =-

M-ndh. (18.48)

Соотношением (18.48) формально вводится магнитный заряд.

Заметим, что взаимодействие электрического и магнитного полей в статике отсутствует. Действительно, величины, входящие в группы соотношений (18.42), (18.38), с одной стороны, и (18.43), (18.44) - с другой, взаимно не пересекаются . Отличие математической структуры этих групп соотношений состоит лишь в том, что плотность магнитных зарядов положена равной нулю.

Уже говорилось о том, что в случае электростатического равновесия заряды проводников сосредоточиваются в тонком поверхностном слое. Если в какой-либо точке внутри проводника напряжённость электрического поля Е отлична от нуля, то в проводнике возникает электрический ток, т. е. движение зарядов. При этом силой тока I называется количество электричества, протекающее через сечение проводника в единицу времени:

(18.49)

Если за любые равные промежутки времени через поперечные сечения проводника проходят одинаковые заряды, ток называется постоянным (по величине и направлению) и обозначается Iq. Согласно закону сохранения заряда (18.19)

/ = -

div (pev) dV = -

PeV ndh.

(18.50)

с силой тока / тесно связан вектор плотности силы тока j, но определяется он различными способами в зависимости от причины, вызывающей ток.

1) Ток называют конвективным в случае переноса заряда плотности Ре СО скоростью V. Тогда

J = -Pev, (18.51)

и из (18.50) имеем

;i8.52)

2) Ток проводимости возникает в случае движения заряда в проводнике под силовым воздействием электрического поля Е. Тогда плотность тока определяется так называемым дифференциальным законом Ома

]=аЁ, (18.53)

где коэффициент а называется проводимостью среды.

3) Из-за изменения со временем векторного поля магнитной индукции D возникает так называемый ток смещения с плотностью

Тогда, пользуясь первым из соотношений электростатики (18.42), запишем

divj = div

1 дЗ\ 1

4тт dt

д dt

dt

;i8.55)

Полный ток j складывается из составляющих, рассмотренных в (18.51), (18.53), (18.54), причём ток проводимости может быть одновременно и конвективным.

Если ток стационарен, то

divj= = 0, j=jn, j = \j\=j.n = jn, a длина j вектора j постоянна. Тогда из (18.56) следует

j ndT, =

;i8.56)

;i8.57)

T. e. вдоль проводника / является постоянной величиной. Отсюда

Jn = \J\ = .

;i8.58)

Предположим, что некоторый тонкий криволинейный проводник длины / с поперечным сечением S соединяет две точ-

ки 1 и 2 сплошной среды (рис. 54). Значения электрического потенциала (р в этих точках обозначим (р\ я (р2. В силу определения (f (18.22), а также равенства (18.52) можно записать

2 2 2

1 - 2 =

Ej dxj =

Eds =

ds = a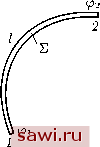

Рис. 54

(18.59)

В цепочке (18.59) использовано скалярное следствие дифференциального закона Ома (18.53) j = аЕ - ds. Поэтому (18.59) часто называют интегральным законом Ома или просто законом Ома:

£ = т, (18.60)

где R = 1/{Т,(у) - сопротивление проводника, £ = -{2 - \) - так называемая электродвижущая сила.

Сформулируем далее закон Ампера, согласно которому сила тока / в замкнутом проводнике L пропорциональна циркуляции Г магнитной напряжённости Н:

г =17.

T = oHds,

(18.61)

где с = 3 10 м/с - скорость света. Проводник L фактически является вихревой линией вектора магнитной напряжённости. Обозначим го{Н = ф и воспользуемся формулой (18.13), выведенной в начале лекции, для выражения Н через ф:

(18.62)

Так как ф dV = ijjdhds = ijjdhds и j i/jdh = Г, то

dh][ о

dsx г А

(18.63)

Соотношение (18.63), связывающее Н и Г, называется законом Био-Савара.