семейство огибающих поля скоростей также прямолинейно и не отличается в пространстве от траекторий частиц.

Если выпустить из каждой точки некоторого замкнутого контура С линию тока (рис. 11), то в пространстве образуется трубка тока.

Для дальнейшего изложения понадобятся некоторые понятия и теоремы векторного анализа [36].

Пусть в ортогональной декартовой системе координат в М с базисными векторами ki заданы векторы: а = afci, Ь = biki, с = Ciki (рис. 12). Напомним два типа умножения векторов а и Ъ.

Рис. 11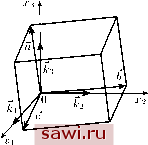

Рис. 12

а) Скалярное произведение векторов. Для базисных векторов ki kj = dij. Тогда

а b = aiki bjkj = aibjdij = aibi. (2.12)

Скалярное произведение двух перпендикулярных векторов равно нулю, кроме того: а -Ь = Ь - а.

б) Векторное произведение векторов. Для базисных векторов ki X kj = Cijkkk, где Cijk - трёхиндексный символ Леви-Чивиты:

123 = 231 = 312 = -213 = -132 = 321 = 1- (2-13)

Остальные же компоненты Cijk, т.е. те компоненты, где хотя бы два индекса одинаковы, равны нулю. Тогда

dxb = aiki X bjkj = eijkaibjkk. (2.14)

Векторное произведение двух коллинеарных векторов равно нулю, кроме того: а хЬ = -Ь х а.

Заметим, что модуль векторного произведения (2.14) векторов а и b численно равен площади S параллелограмма, натянутого на эти векторы (рис. 12):

а X Ь I = а Ь I sina = И. (2.15)

Вводя единичный вектор нормали п к поверхности И,

п = riiki, п = щщ = 1,

(2.16)

О Справедлива теорема Гельмгольца: всякое векторное поле а(х, t) может быть однозначно (с точностью до функции времени) представлено в виде: а = grad (р + го{ф.

можно определить площадь S как векторную величину:

(2.17)

в) Смешанное произведение трёх векторов.

{а хЬ) с = (Ь X с) а = (с х а) - Ь = CijkaibjCk (2.18)

Модуль величины (2.18) представляет собой объём V параллелепипеда, натянутого на векторы а, b и с (рис. 12):

V=\{axb)c\ = \e,jkabjCk\ = S с . (2.19)

Смешанное произведение трёх компланарных векторов равно нулю.

Введём в рассмотрение дифференциальный оператор V - набла. Его компонентами являются операторы частного дифференцирования:

V = -кг = дгкг. (2.20)

Применяя рассмотренные выше виды умножения к V, получим V а = djki ajkj = Sijdjaj = djaj = diva, (2.21)

V X a = Sifci X ajkj = ekkdiaj = rota, (2.22)

V(/9 = = grad(/9, (2.23)

где (/9(xi, X2, Хз) - некоторая скалярная функция.

Векторное яоув а(х1,Х2,хз) называется потенциальным, если существует такое скалярное поле (/(хьХ2,хз), что

а = grad(/9. (2.24)

Поле (/9 носит название скалярного потенциала а.

Векторное поле а(х1,Х2,хз) называется соленоидальным, если существует такое векторное поле 0(xi,Х2,хз), что

а = rot. (2.25)

Поле ф носит название векторного потенциала а О .

Дифференциальные операторы diva и rota называются дивергенцией и ротором векторного поля а, а оператор grad(/9 -

градиентом скалярного поля Lp. В дальнейшем выясним механический смысл введёных дифференциальных операторов, а пока определим линейный оператор второго порядка

А(/9 = div grad(/9, (2.26)

называемый оператором Лапласа скалярного поля Lp.

Докажем, что для любых скалярного поля Lp и векторного поля а выполняются тождества

а) div rot а = О, б) rot grad (/9 = 0. (2.27)

Воспользуемся определениями (2.21)-(2.23).

а) div rot а = div (cijkdiajkk) = edidkaj = О, в силу того что символ Леви-Чивиты еф антисимметричен по индексам i и к (см. (2.13)), а смешанная производная didkdj по i и fc симметрична. Следовательно, их свёртка по этим индексам равна нулю.

б) rot grad (/9 = rot ikidiLp) = Cjikdidjifh = 0.

Для того чтобы поле а было потенциально, необходимо и достаточно, чтобы rota = О, а для того чтобы оно было соленои-дально, необходимо и достаточно, чтобы diva = 0. Если поле а одновременно потенциально и соленоидально, то его скалярный потенциал, очевидно, является гармонической функцией, т. е. удовлетворяет уравнению Лапласа

= О, (2.28)

и наоборот, любой гармонической функции можно поставить в соответствие векторное поле, являющееся и потенциальным, и соленоидальным [20].

Рассмотрим теперь в качестве а поле вектора скорости v{x\,X2,xs,t)- Все ранее сформулированные определения и утверждения применимы теперь к v. Скалярный и векторный потенциалы скорости будем по-прежнему обозначать (риф соответственно. Введём также в рассмотрение вектор вихря и:

ш = rotv, (2.29)

являющийся, очевидно, соленоидальным. Векторные линии поля Uj{x\,X2,x,t) носят название вихревых линий. Если же из каждой точки замкнутого контура выпустить вихревую линию, то в пространстве образуется так называемая вихревая трубка.

Свяжем с вектором вихря антисимметричный тензор вихря, или спин-тензор, и:

(ij = ijk(k (2.30)