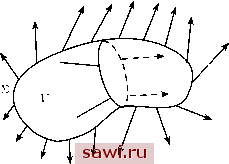а(ж1,Ж2,жз)

Рис. 15

Из (2.42) видно, что для соленоидального векторного поля поток через любую замкнутую поверхность равен нулю. Отметим также, что все предыдущие рассуждения и формула Остроградского-Гаусса имеют место и для нестационарного векторного поля a(xi, Х2, Хз, t) в каждый момент времени t.

Пусть теперь а является полем скоростей i7(xi,Х2,хз) в теле У, так что

div V dV =

V vdV. (2.45)

Если V потенциально и Lp - скалярный потенциал, то, подставляя равенство v= grad(/9= V(/9 в (2.45), получим для Lp первую формулу Грина:

grad Lp ndYi =

AdV. (2.46)

Здесь Аф - оператор Лапласа, определённый в (2.26).

Величина дс/д1, равная скалярному произведению градиента поля с на единичный вектор /, соответствующий некоторому направлению в пространстве, называется производной с по этому направлению. Таким образом, под знаком поверхностного интеграла в (2.46) стоит производная (р по нормали, или нормальная производная Lp, в точках поверхности S (она обозначена д(р/дп).

Представим далее скорость в виде v = (р\ gr3id(p2, или, покомпонентно: Vj = (p\di(p2, и подставим в (2.45). Получим

вторую формулу Грина:

д(р2

{di(p\di(p2 + (p\didi(p2) dV =

grad Lp\ grad Lp2 + 2) dV. (2.47)

Записав вторую формулу Грина для v = (/92grad(/9i и вычитая её из (2.47), получим

dLp2

2

{iA2-2\)dV. (2.48)

Соотношение (2.48) носит название третьей формулы Грина.

Рассмотрим в качестве примера потенциальное течение со скалярным потенциалом

= -

47ГГ

Q = const, г = xf + + = уад . (2.49)

Найдём линии тока и эквипотенциальные поверхности, а также поток вектора скорости через поверхность сферы Та- = cl-

Эквипотенциальными поверхностями (поверхностями Lp = const) для течения (2.49) являются концентрические сферы г = const с центром в точке О (рис. 16). Следовательно, линиями тока будут лучи, исходящие из точки О. Действительно, найдём поле скоростей:

д(р Q дг Q Xi Qxi

dxi Аттг dxi Аттг г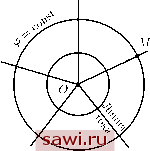

Рис. 16

(2.50)

Компоненты щ единичной внешней нормали к поверхности сферы будут направляющими косинусами радиуса-вектора, т. е. щ = Xi/a. Тогда

)Xi Xi

С другой стороны, на поверхности

(2.5i;

Из сравнения (2.51) и (2.52) следует, что \v\ = \v\. Поэтому в любой точке М вектор скорости направлен по нормали к сфере, проходящей через точку М, т.е. к соответствующей эквипотенциальной поверхности. Линиями тока и траекториями будут лучи, выходящие из точки О. Движение со скалярным потенциалом (2.49) называется пространственным источником-стоком. В случае Q > О имеем источник в начале координат (скорости всех частиц согласно (2.51) направлены от центра), в случае Q <0 - сток (скорости всех частиц направлены к центру).

Поток через поверхность сферы равен

Sa = Q, (2.53)

47га2

где iSal = 47га - площадь поверхности сферы Ид. Видно, что величина V, равная Q, не зависит от радиуса а и характеризует течение как целое. Эта характеристика называется расходом пространственного источника-стока.

Вычислим теперь оператор Лапласа потенциала (р (2.49):

1 \ д 1 3>XiXi 3 3 О

5 3 3 3

A(f = - Д- = О везде, кроме г = 0.

47Г Г

Но исходя из (2.53) и первой формулы Грина (2.46) можно показать, что интеграл от А(р по любому шару Va с поверхностью Ид равен Q и не зависит от а.

Таким образом, А(р - необычная функция: она равна нулю везде, кроме начала координат, но интеграл от неё по любому шару с центром в начале координат равен Q 0. Функция А(р представляет простейший пример обобщённой функции {дельта-функции). (О правилах использования дельта-функции см. [42].)

Выберем некоторую кривую, соединяющую точки А и В (рис. 17), и назовём циркуляцией Гав векторного поля а(х1,Х2,хз) вдоль

Рис. 17