Рассмотрим криволинейный параллелепипед, образованный координатными поверхностями (рис. 5):

1 = const, qi + dqi = const;

<72 = const, 2 + = const; (4.2)

3 = const, 3 + dqj = const.

Ребра этого параллелепипеда dsu ds2, dss есть элементы дуг, соответствующие приращению координат dqu dq2, dqz-

dsi = Hidqi, ds2H2dq2, ds3 = H3dq3. (4.3)

Здесь Ни Hi, Яз - коэффициенты Ламе:

{i=\, 2, 3).

(4.4)

Объем параллелепипеда в предположении ортогональности координат будет равен

dx = dsi ds2 ds3 - H1H2H3 dqi dq2 dq. (4.5)

Для того чтобы записать закон сохранения массы, подсчитаем изменение массы бМ за время dt внутри элементарного параллелепипеда двумя способами.

I. В момент времени t масса жидкости ДМ в объеме dx равна

ДМ = р 1/ dsi ds2 dSi =

= p\tHiH2H3 dqidqz dq.

В момент времени t -f Д/ масса жидкости в том же объеме dx будет

ДМ = р \t+cit dsx ds2 dss =

= P \t+dt H1H2H3 dqi dq2 dq.

Изменение массы в объеме dx за время dt

m = AM-AM = {p\t+dt-

- pldHiHzHsdqidqidqs. (4.6)

Из равенства (4.6) следует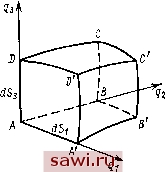

Рис. 5.

бМ = -If Н1Н2Н3 dqi dq2 dq3 dt.

(4.7)

2. Изменение массы в рассматриваемом объеме за время dt может быть связано с тем, что есть источники, распределенные в пространстве, и что количество жидкости, которое втекло в объем dx, не равно количеству жидкости, которое вытекло из этого объема.

Введем обозначения:

8т - изменение массы в объеме dx за счет источников;

Smi - Изменение массы в объеме dx за счет того, что через грань ABCD могло вытечь не такое количество жидкости, которое втекло через грань ABCD;

б/пг - изменение массы за счет протекания через грани AADD и ВВСС;

8тз - изменение массы за счет протекания через грани ААВВ и DDCC.

Общее изменение массы 8М

(4.8)

По определению величины q имеем

bm = qdxdt - qHiHiH dqi dq2 dq dt. (4.9)

Подсчитаем Ш\, Ш2, б/пз. Для этого обозначим через Vu Сг, V3 проекции скорости жидкости на оси qi, 2. з- Через грань ABCD в объем dx за dt поступает масса жидкости

6Mi = (р ds2 dSsVi dt) = (рУ1Я2Яз) dq2 dq dt. Через грань ABCDза то же время вытекает масса жидкости

6M( = (p dsdsvdt) Интересующая- нас величина

-{9V,H,H,)\Jq,dq,dt.

dqdq,dt =

Аналогично получим

= -(pv,H2H3)dq,dq2dq3dt. (4.10)

Ьт2= - -д(9V2H1H3) dqi dq2 dqs dt;

(РУ3Я1Я2) dqi dq2 dqs dt.

бтз = -

(4.11) (4.12)

Общее изменение массы 6М получим, подставив (4.9) - (4.12) в (4.8):

-(р.,Я2Яз)-(рс;2Я,Яз).

ipV3H,H2) +

+ qHiH2H3 dqidq2dq3dt. (4.13)

Сравнивая два выражения (4.7) и (4.13) для 8М, получаем уравнение неразрывности в криволинейных координатах

Я.ЯгЯз + {тН2Нз) + 3 (тННз) +

+ -{pv3HxH2)==qH,H2H3. (4.14)

Рассмотрим частные случаи.

а) Декартовы координаты х, у, z. Здесь

Ц\ = х, q2 = y, 93 = z; Hi = Н2 = Нз=1. Уравнение (4.14) примет вид

б) Цилиндрические координаты (г, 9, г). Здесь

qi = r, ?2=9, q:i = Z; Vi-=Vr, V2=Vq, V3=Vz.

Связь между цилиндрическими и декартовыми координатами имеет вид

x = rcQsQ, y = rsinQ, z = z. Коэффициенты Ламе, вычисленные по формулам (4.4): Hi = Hr=l, Я2 = Яе = г, Яз = Яг=1.

Уравнение неразрывности в цилиндрических координатах запишется в виде

в) Сферические координаты (г, 9, Л). В этом случае qi = r, 92==9, з = Л; Vi = Vr, V2 = Vq, VsVt,;

л: = г sin 9 cos Л, = г sin 9 sin Л, 2 = rcosA.

Коэффициенты ЛамеНх = Нг=\, Н2 - Н = г, Нз = Нх = гsin9, Уравнение (4.14) в сферических координатах примет вид

;.2 sin ef + (ру,2 В) + (рг sin 9) +

+ (pfxr) = ?r2sin9. (4.17

Обратимся к общему уравнению (4.14). Будем дифференцировать произведения, отделяя множители, содержащие р, и разделим затем все члены на ЯЯг-Яз. Получим

£р . fi ар . щ др . Vj dp dt Я1 3(7, Я2 5(72 Яз (3(7з

+ -Я[1?7(з) +1-(2Я,Яз) -f (.зЯ,Я2)]=,

(4.18

Рассмотрим первые четыре слагаемых и учтем при этом (4.3)