Проинтегрировав (2.3) от ti до /г, получим запись закона количества движения для конечного промежутка времени

dt. (2.4)

Изменение количества движения за некоторый промежуток времени равно сумме импульса массовых сил и импульса поверхностных сил.

Обратимся к равенству (2.3). Для дифференцирования объемного интеграла имеем формулу (15.7) гл. I. Положив в ней-А = pv, получим

d dt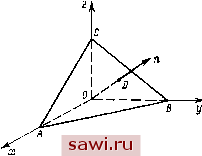

Рис. 6.

-S)S( + Pvdivv)d..

(2.5)

Принимая во внимание (2.5), перепишем (2.3) в виде

+ pv div V - pF с?т = T dS.

(2.6)

Равенства (2.3), (2.4), (2.6) дают интегральную запись закона количества движения.

§ 3. ФОРМУЛА КОШИ

Запишем закон количества движения для частного случая объема т. За объем т выберем тетраэдр, три грани которого параллельны координатным плоскостям (рис. 6). Обозначим площади этих граней через Sx, Sy, Sz- Внешние нормали к этим граням направлены противоположно осям Ох, Оу, Oz. Площадь четвертой грани с нормалью п обозначим через Sn. Пусть т-., т-у, T z, т,! - напряжения, действующие на каждую из граней.

Применив формулу (2.6) к объему т, будем иметь

SSS[4-(Pv) + Pvdivv-pF

dx =

\\r ,dS+x ydS+t ,dS+\\x,dS. (3.1)

Т - 1 Хух fyy Туг

§ 4. ТЕНЗОР НАПРЯЖЕНИИ

Будем исходить из формулы Кош1 (3.7). Докажем, что таблица (3.8) является аффинным ортогональным тензором второго ранга. Для этого надо найти формулы преобразования xik при переходе от одной системы координат х, у, г к другой х, у\ г\ Обозначим орты координатных осей соответственно через i, j, к и i. У, к. Вспомним таблицу (7.1) гл. 1 для направляющих косинусов а;к и будем пользоваться формулой Коши, выбирая за п последовательно i, j, к. Получим

tx = f.vaii + Tjuis + Tai3; (4.1)

iy = tx\ + Tjnja + Тг 2з; (4.2)

T = т аз[ -f- Tj,a,2 -f- таз. (4,3)

Рассмотрим одну из этих формам, например (4.1). Представим Tj,- через проекции хх, ху, r/z на оси х, у\ г:

T. = i4; -f j4, + k4,. (4.4)

Соответственно т т - через проекции на оси х, у, z:

Г* = Ихл: +JTxy + кТг,

Ту = iTjfx + IXyy + кху, (4,5)

Подставляя (4.4) и (4.5) в (4.1), получаем векторное равенство T;(i + ХхуУ + ХхЛ = а (Ti -f Xxyi + ХхЛ) +

4- 12 (yxi + bui + ff*) + (. + i/i + zz- (4.6)

Умножая последовательно (4.6) скалярно на i, j, к, получим выражения для т, г, х-- через составляющие таблицы Т в координатах {х,у,г). Выпишем одно из равенств (заметим, что (i-l)-an. (i-j)=ai2. (r-k)=ai3):

+ ai2 llyj + l20l2lyy -f laOlsyz +

+ CigauT + cdaOiaTsj, + aijOriTz. (4.7)

Используя (4.2) n (4.3), получаем аналогичные выражения для остальных шести составляющих. Из равенства (4.7) видно, что составляющие таблицы Т при переходе от одной системы

(3.8)

<-гу

(3.8)

§ 4. ТЕНЗОР НАПРЯЖЕНИЙ

Будем исходить из формулы Коши (3.7). Докажем, что таблица (3.8) является аффинным ортогональным тензором второго ранга. Для этого надо найти формулы преобразования т,* при переходе от одной системы координат х, у, z к другой х, у, г. Обозначим орты координатных осей соответственно через i, j, к и i, у, к. Вспомним таблицу (7.1) гл. 1 для направляющих косинусов aik и будем пользоваться формулой Коши, выбирая за п последовательно i, j, к. Получим

ty = T.a2i + i/ 22 + Тг 23;

(4.1) (4.2) (4.3)

Рассмотрим одну из этих формул, например (4.1). Представим через проекции х,.х, Хху, Гхг на оси х, у, z:

Соответственно г.

- = i4x + j4, + k4v. (4.4)

ty, - через проекции на оси х, у, z:

х - хх Л ixy ~Ь кТд;2,

Ту = \Хух + \Хуу + кху, (4.5)

Подставляя (4.4) и (4.5) в (4.1), получаем векторное равенство -хх + -xyY + Тхгк = а {Ххх\ + Хху] + тк) +

+ 12 {-ух + -Суу] + Tzk) + 13 (Т + Tzyj + Тгк). (4.6)

Умножая последовательно (4.6) скалярно на V, ], к, получим выражения для Ххх, ху, хг через составляющие таблицы Т в координатах {x,y,z). Выпишем одно из равенств (заметим, что (i-i)=aii, (i-j) = ai2, (i-k)=ai3):

Ххх = ацО-цХхх + Щ1Щ2т:ху + иаихг +

+ ai2aiiTj;x + ai2ai2Tjy + ai2ai3Tj,2 +

+ СЦзацТгх + ai3ai2Tzj/ + [зТгг. (4.7)

Используя (4.2) и (4.3), получаем аналогичные выражения для остальных шести составляющих. Из равенства (4.7) видно, что составляющие таблицы Т при переходе от одной системы

Тхх Тху хг