координат к другой преобразуются как компоненты аффинного ортогонального тензора второго ранга. Тензор Т = т,* называется тензором напряжений.

Физический смысл компонент тензора напряжений очевиден. Возьмем вектор Хх - напряжение на площадку, перпендикулярную оси X (рис. 8):

Здесь ххх - нормальное напряжение; хху, Ххг, являющиеся проекциями вектора Хх на оси координат у и г, есть напряжения, касательные к площадке.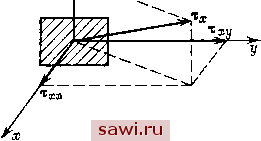

Рис. 8.

Таким образом, диагональные компоненты тензора дают нормальные составляющие напряжений, боковые компоненты дают касательные составляющие напряжений, приложенных к площадкам, перпендикулярным осям координат.

§ 5. ДИФФЕРЕНЦИАЛЬНАЯ ЗАПИСЬ ЗАКОНА КОЛИЧЕСТВА ДВИЖЕНИЯ

Исходим из интегральной записи закона (2.6)

\\\[4г (pv) + pv div V - pF] rfT = 5 5 т dS.

(5.1)

Используя для тл формулу Киши, преобразуем интеграл по S в правой части (5.1) к интегралу по объему т, применяя фор-

мулу Гаусса - Остроградского:

т dS = [Т;( cos (и, х) + Ху cos (гСу) + cos (nz)] dS ==

Подставляя (5.2) в (5.1), получаем интегральную запись закона в виде

pv + pv div V - pF - - -

dT = 0. (5.3).

Так как (5.3) имеет место для любого объема т, то, следовательно,

-pv + pvdivv-pF--- = 0. (5.4)

Выполнив дифференцирование в первом слагаемом, можем переписать (5.4) в виде

dv /dp \ <3т, дх дх.

Равенства (5.4), (5.5) представляют собой дифференциальную запись закона количества движения в общем случае.

Предположим, что движение сплошной среды происходит при отсутствии источников массы, т. е. == 0. В этом случае уравнение неразрывности имеет вид (2.6) гл. II. Учитывая это, получим запись закона количества движения в векторной форме:

dv дх дх дх,

= pF+-f-+. (5.6)

dt дх ду dz

или в проекциях на оси координат:

dt р\ дх ду дг J

-F ЦЛ-Л Г561

dt р \ дх dz ) -1

I (хг , dXy дх\ dt р \ дх ду dz )

Слева в уравнениях (5.6) стоит оператор полной производной. Уравнение (5.6) или эквивалентную ему систему уравнений (5.6) обычно называют уравнениями движения сплошной среды в напряжениях.

Замечание 1. Запись закона количества движения в интегральном виде дается равенством (5.3). При отсутствии

источников массы справедливо равенство (2.6) гл. II, в силу чего закон количества движения (5.3) запишется в виде

т IS

555(pF-pw)rfT + 55T rfS = 0, (5.7)

т. е. в каждый момент времени сумма всех сил, приложенных к выделенному объему жидкости, включая и силы инерции, равна нулю.

Замечание 2. Из второго закона Ньютона, записанного для точки = F, следует, что скорость образования количества движения равна силе, т. е. сила - источник, из которого образуется количество движения. С указанной выше точки зрения изменение количества движения в объеме жидкости т происходит по двум причинам: за счет объемного выделения импульса, порожденного массовой силой, и за счет потока импульса через границу области.