ГЛАВА V ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ

Для записи такого фундаментального физического закона, как закон сохранения энергии, необходимо установить, из каких видов энергии складывается полная энергия жидкого объема, определить виды притоков энергии извне и учесть превращения одного вила энергии в другой.

§ 1. ВНУТРЕННЯЯ ЭНЕРГИЯ

Рассмотрим сначала некоторую покоящуюся однородную массу жидкости М в объеме т. Пусть О означает ее исходное состояние, которое, вообще говоря, определяется некоторым набором параметров (например, давлением, температурой и др.). В результате нагрева, сжатия и других воздействий масса жидкости перейдет в новое состояние, определяемое другими значениями параметров. Переход массы жидкости из исходного положения О в другое связан с изменением AS энергии. Будем считать, что в исходном состоянии масса М имела запас энергии So. Тогда можно ввести величину

Jf = o + A- (1.1)

Если каким-то образом выбрана величина So и известно AS (экспериментально или теоретически), то для любого нового состояния величина S может быть определена по формуле (1.1). Таким образом, через AS определяется величина внутренней энергии S данной массы жидкости. Естественно ввести величину Е - внутреннюю энергию, отнесенную к единице массы. В общем случае неоднородной движущейся жидкости Е - функция координат и времени:

£ = lim£,p = lim. (1.2)

Из определения (1.2) следует, что запас внутренней энергии в массе dm равен dS = Edm = Epdx. Внутренняя энергия конечной массы жидкости в объеме т

S=\l\pEdx. (1.3)

Выражение для Е обычно известно из физики. Для совершенного газа, находящегося в состоянии тер.модинамического равновесия, уравнение состояния которого есть уравнение Клапейрона р = pRT, внутренняя энергия зависит только от температуры. Выражение для внутренней энергии имеет вид

E=YCvdT, где Cv - теплоемкость при постоянном объеме.

Здесь в качестве исходного берется состояние, в котором абсолютная температура равна нулю. Когда нет процессов диссоциации и ионизации, внутренняя энергия состоит из энергии поступательного Еп, вращательного Ер и колебательного Ек движений молекул. Для одноатомного газа - const и Е = Е =

=у/?Г.Для случая двухатомного газа в определенном диапазоне температур (для кислорода и азота примерно при температурах не выше 600-700 К и не слишком низких температурах), когда практически возбуждены только поступательные и вращательные энергии молекул, теплоемкость постоянна и

Е = Еа +Ep = Y более высоких температурах начи-

нает сказываться возбуждение колебательной энергии молекул. Теплоемкость с колебательных степеней свободы зависит от температуры, и внутренняя энергия может быть представлена

ST 5 ст

Cv dT = -RT -\- \ Со dT. Зависимость с от Т о JO

известна. Для многоатомных газов вид функций Евр и от Т будет зависеть не только от числа атомов, но и от структуры молекулы.

§ 2. ПОЛНАЯ ЭНЕРГИЯ

Если жидкость движется, то она обладает кинетической энергией. Кинетическая энергия dT : массы dm, движущейся со скоростью V, равна Й7к = dm--==- dr. Кинетическая энергия массы, заключенной в объеме т:

й. (2.1)

Полной энергией называется сумма кинетической и внутренней энергий данной массы газа

и = Т, + , U=\\\p[- + E)dx. (2.2)

§ 3. ИНТЕГРАЛЬНАЯ ЗАПИСЬ ЗАКОНА СОХРАНЕНИЯ ЭНЕРГИИ

Изменение полной энергии некоторой массы жидкости за промежуток времени от /] до 2 происходит за счет работы массовых и поверхностных сил, за счет притока за тот же промежуток времени тепловой энергии вследствие наличия объемно-распределенных источников тепла, а также притока тепла через поверхность. Если обозначить через Ах работу массовых сил. As - работу поверхностных сил, Qt - объемное поступление энергии, Qs - количество тепла, поступившее через поверхность

за время от ti до /2. то закон сохранения энергии запишется в виде

и - и I,- = A,+ As + Qr + Qs- (3.1)

Здесь U\t - значение полной энергии в момент времени t.B соответствии с определением полной энергии имеем

С,.,-У,.,=

t-i,

(3.2)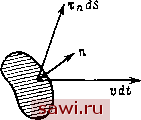

Вычислим слагаемые, входящие в правую часть (3.1).

Работа массовых сил. Обозначим через АЛт работу за промежуток времени dt массовых сил, приложенных к массе в объеме т. На массу dm в объеме dx действует сила pFdx. Перемещение этой массы за время dt есть dr = vdt. Работа указанной силы на перемещении dr равна p(F-v)dx dt, откуда следует, что

ЛЛ = Л JJJp(F-v)cfT.

Работа, совершенная массовыми силами за конечный промежуток времени от ti до /2. будет

A=-\ldt\\\piF..)dx. (3.3)

Работа поверхностных сил. На элемент поверхности dS с нормалью п действует сила XndS (рис. 9). Работа этой силы за время dt равна {rnv)dSdt, и, следовательно, работа сил, приложенных ко всей поверхности S, будет

AA5=*55(T .v)dS.

Работа поверхностных сил за конечный промежуток времени (/ь /2)

As = \dt\\{r,.y)dS. (3.4)

Объемное поглощение энергии. Иногда приходится учитывать поглощение (или выделение) энергии каждым элементом объема жидкости. Не указывая конкретных причин поглощения или выделения энергии, будем учитывать этот факт следующим образом. Обозначим через edxdt количество тепла, поступившего в объем dx за время dt. Величину е, имеющую смысл секундного притока тепла, отнесенного к единице объема, назовем скоростью объемного поглощения энергии. Энергия,

3 Зак. 1031