Система уравнений (1.1) -(1.5) в силу (1.7) и (1.8) примет вид

др dt

ар dx

dx dVx

dVu ,

(1.10)

(1.11)

dxdij P = Ф ip)-

В этой системе три уравнения и пять неизвестных функций. Преобразуем уравнение (1.10) так, чтобы из него исчезли Vy п Vz, и тем самым получим систему трех уравнений для определения интересующих нас величин (1.7) и (1.8).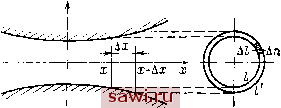

Рис. 15.

Проинтегрируем уравнение (1.10) по поперечному сечению трубы F:

dp dp dvx

L dt

(dVn dVz V

dS = 0. (1.12)

Три первых слагаемых не зависят от г/ и г, поэтому (1.12) можно переписать в виде

Преобразуем интеграл в формуле (1.13). Учитывая, что р постоянно по сечению: p = p{x,t), и вводя вектор поперечной скорости и = Vy] -\- Vek, получаем

]\9{+ )dS = 9\]<iiv и dS = pUndl. (1.14)

F F I

Перемещение частиц за время Д/ можно представить как сумму перемещения вдоль оси х иа расстояние Дх = Vx At и перемещения в поперечной плоскости и At (рис. 15). Частицы с контура / перейдут на контур /. Расстояние по нормали от / до I равно Дп = UnAt. Изменение площади равно площади кольца

AF AndlAtUndl, ndl= V\m ~ = (1.15)

Заменяя в (1.13) согласно (1-14) лвойнон интеграл криволинейным и учитывая (1.15), получаем

, , dF дР

Считая, что труоа не деформируется, т. - ~jj - x~gj < запишем (1.16) в виде

Отсюда окончательно получи.м

уравнения (1.18), (1.9) и (1.11) образуют систему уравнений для отыскания Vx, р, р. Для установившихся течений эта система приобретает вид

A(p,f) = 0, vx + l = 0, р = Ф(р). (1.19)

Уравнения (1.19) могут быть легко проинтегрированы. Решение задачи об одномерном установившемся движении жидкости получим в виде

pFVx = Cu - + J- = C2, Р = Ф(р). (1.20)

Второе уравнение в (1.20) есть запись интеграла Бернулли для полученного приближенного решения задачи. Пренебрежение поперечными ускорениями, принятое вначале, равносильно тому, что в выражении для мы пренебрегаем величиной -f у по сравнению с и.

Так, например, если взять трубу с углом полураствора а, таким, что tga<0,l, то + иу < 0,01, т. е. указанное рассмотрение дает точность порядка одного процента.

§ 2. ДВИЖЕНИЕ НЕСЖИМАЕМОЙ ЖИДКОСТИ В ТРУБЕ ПЕРЕМЕННОГО СЕЧЕНИЯ

Для несжимаемой жидкости р = рд = const. Площадь F - F(x) задана. Решение имеет вид

VxF = A, + = В, р = ро. (2.1)

Отсюда

Постоянные Л и В определяются по заданным характеристикам в некотором сечении. Так, при х = Xq (F (х) = F (xq) = Fq)

должны быть заданы у,. 1 = v!, = А,. Вместо скорости

можно задать расход Q = PoVlF. Из решения видно, что с увеличением сечения F скорость Vx убывает, давление возрастает.

§ 3. ДВИЖЕНИЕ СЖИМАЕМОЙ ЖИДКОСТИ В ТРУБЕ ПЕРЕМЕННОГО СЕЧЕНИЯ. СОПЛО ЛАВАЛЯ

Формулы (1.20) дают общее решение задачи. Постоянные, содержащиеся в этом решении, находятся по данным гидродинамическим элементам в некотором сечении. Постоянная Cj = = Q - расход жидкости. Из (1.20) все интересующие нас величины Vx, р, р могут быть .найдены в любом сечении F - F{x). Решение закончено. Однако здесь интересно исследовать характер течения. Для этого прологарифмируем и затем продифференцируем первое равенство из (1.20), а второе равенство запишем в дифференциальном виде. Тогда будем иметь

+ - + = 0; (3.1)

VxdVx + = 0. (3.2)

Используя соотношение р = ф(р), можем найти Известно,

что = квадрат скорости звука. Подставляя dp = а?йр в уравнение (3.2), получаем

a- dvx, -dvx. (3.3)

Равенство (3.1) с учетом (3.3) можно переписать в виде

\а Ч Vx ~ F

(3.4)

Соотношение (3.4) позволяет сделать ряд выводов. Будем для определенности считать Vx > 0. Знак скобки в (3.4) зависит от того, с каким течением мы имеем дело.

1. Пусть М = -< 1,т. е. < а,-скорость течения меньше скорости звука. Тогда если площадь F уменьшается, dF < О, то dVx>Q - скорость увеличивается. Если dF>0 - сечение увеличивается, то du < О - скорость уменьшается.

2. Пусть М = -> 1,г. е. t,v > а,-скорость потока больше

скорости звука. В этом случае если dF < О, то и dvx < О, т. е. с уменьшением сечения уменьшается скорость. Если diF > О, то н dvx > О - увеличение сечения ведет к увеличению скорости.

Таким образом, в дозвуковом потоке, как и в несжимаемой жидкости, уменьшение сечения ведет к увеличению скорости, и