Для плоского течения имеется простая связь между функцией тока и вихрем скорости

dv dvx (Эф д*1

= --Ж = -- = - (3.10)

Если движение безвихревое (Q = 0), то г] удовлетворяет уравнению Лапласа

А = 0. (3.11)

Уравнение (3.11) служит для нахождения функции iji при соответствующих граничных условиях. Пусть жидкость обтекает непроницаемую поверхность тела. На этой поверхности t) == 0. Запишем это условие через функцию г), используя (3.3) и (3.8):

--= ... cos (Г.) + cos (G) = 4 4 + 47 = 41- (3.12) Получаем, что на контуре тела должно быть выполнено условие 4j- =0, т.е. 115 15== const - функция тока - сохраняет постоянное значение на s. Это означает, что граница тела должна быть линией тока. Физически это очевидно.

Таким образом, в случае безвихревого движения функция тока г: может быть найдена как решение уравнения Лапласа (3.11), удовлетворяющее граничным условиям на бесконечности и на поверхности тела:

l--vy, fL = .., {x,y)\s = C. (3.13)

Задача отыскания решения уравнения Лапласа по заданному значению функции на границе называется задачей Дирихле. Для внешней задачи Дирихле условия имеют вид (3.13).

Обратим внимание еще раз на то, что если потенцршл скоростей существует только когда движение безвихревое, то функция тока существует всегда. При безвихревом движении функция тока удовлетворяет уравнению Лапласа.

§ 4. КОМПЛЕКСНЫЙ ПОТЕНЦИАЛ И КОМПЛЕКСНАЯ СКОРОСТЬ

Мы получили выражения (2.3) и (3.3) для проекций скорости через производные от функций ф и Сравнивая (2.3) и (3.3), получаем уравнения связи между потенциалом скоростей и функцией тока

аф аф аф а1)з .

дх ду ду Jx

Это известные из теории функций комплексного переменного условия Коши - Римана, которые гарантируют, что функция

Ю = Ф (л:, у) + /11: [х, у)

Пример 3.

(5.1)

где q вещественно.

Рассмотрение этого прп.мера удобнее вести в полярны.х координатах г, 6:

Z = X-jr iy = гс*, r = \z\, 6=arg2, w{z) = (f + ii = (\nr + iQ),

Линии тока = const будут лучами, выходящими из начала координат. Линии равного потенциала ф = const есть окружности г = const (рис. 18).

tj)=const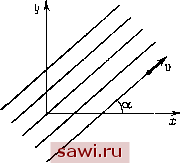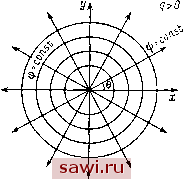

Рис. 17.

Рпс. 18.

Замечание о вычислении скоростей потенциального потока в криволинейных координатах. Пусть имеется потенциал скоростей ф. Тогда

у = дга(1ф,

vi = {v ]) = Vx cos iCx) + Vy cos (/, y) + Vz cos (/, z) =

= cos iCx) + cos Су) + 4J cos iCz) = .

Пусть q\, q2, q- криволинейные ортогональные координаты. Элементы дуг dsi, соответствующие приращению координаты qi, равны dsi = Hidqi, где Я,- - коэффициенты Ламе. Проекции

, I <5ф

скоростей вычисляются по формулам =-- .

Для цилиндрических координат q] = г, 92 = Э, 93 = г коэффициенты Ламе равны Я] = 1, 2= г, Я3 = 1 и проекции скоростей запишутся в виде

дц> (Зф (5ф 1 5ф (Эф Зф

(Э5, ~ (Эг ~ asT ~ Т аёГ ~ as аГ Вернемся к рассмотрению течения, определяемого комплексным потенциалом ia{z) = ~\nz. Проекции скоростей на оси полярных координат будут

-, = i£ - L дг 2л г

1 аф

Отсюда видно, что скорость постоянна по величине на кал<дой окружности с центром в начале координат, направлена по радиусу и убывает с ростом расстояния г. При 9 > О скорость направлена от центра (у, > 0), при q < <0 - к центру {Vr <()). Формула (5.1) дает комплексный потенциал течения от источника (стока), рас-полол<енного в начале координат.

Выясним смысл величины 9. Подсчитаем расход жидкости Q через контур, охватывающий начало координат. Записывая интеграл по замкнутому контуру как интеграл от А до В, где Л и В - совпадающие точки контура, получим

Q = ( о ds = dl]: = \\->в - 1), = 2n = q.

Таким образом, q - обильность источника. При q>0 имеем источник, при q <i О - сток (источник отрицательной обильности). Если источник расположен не в начале координат, а в точке 2 = а, то комплексный потенциал будет иметь вид

(г) =

In (2 - а).

Пример 4. Пусть в точке А плоскости (х,у) расположен источник обильности q, в точке В - источник обильности -q (сток), причем комплексные координаты точек (рнс. 19)

2л = у Zb= 2

Комплексный потенциал течения, вызываемого каждым из источников, имеет вид

, = - 4- е .

£в(2) = --1п(2 + 4е-).