Комплексный потенциал суммарного течения w{z)-=Wa {z) + Wb (z),

-(г) = 1п

Предположим, мы рассматриваем такую точку г, что Тогда, раскладывая логарифмы в ряды по -, получаем

z\ > /.

w{z)=-

2я V 2z 2z )--

2n z +

Пусть /->-0, a обильность q->oo, причем так, чтобы произведение ql оставалось постоянным; ql = М. Тогда для такого

предельного течения комплексный потенциал будет иметь вид

ф = С0Т151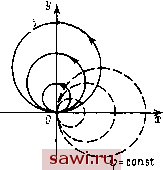

Рис. 20.

() = -Т - (5.2)

Формула (5.2) дает комплексный потенциал течения от расположенного в начале координат диполя с моментом М и осью диполя, образующей угол а с осью х. Ось диполя принято направлять от стока к источнику.

Изучим картину течения от диполя. Не уменьшая общности, положим а = О, т. е. рассмотрим диполь, координат, ось которого совпадает

расположенный в начале

с осью Ох (рис. 20). Функции 01(2), ф, будут иметь вид

гп -и /тП - -

(г) = - - - , ф -f гг; = -

Ф = -

2л х} + if

X - ly 2я х + у

(5.3)

2я х + у

Линии тока if) = const есть линии, на которых

х + у

- rl2 = г2

Линии тока - окружности, проходящие через начало координат, центры которых лежат на оси у. Аналогично линии равного потенциала ф = const - окружности [х - с)2 + (/ = с, проходящие через начало координат с центрами на оси х. Скорости

легко вычислить, имея (5.3). Если а О, то вся картина поворачивается на угол а. Если диполь расположен в точке z = а,

то w (г) = -

2я z - а Пример 5.

(5.4)

В полярны.х координатах

т-(г)=2(1пг + /9) = 0-/1пт,

Го, Г ,

4 = 19, г; = --1пг.

Линии тока = const есть окружности с центром в начале координат, линии ф = const есть лучи 6 = const (рис. 21). Частицы жидкости переме-

щаются по скоростями

окружностям со

Г>0

9 =

d(f \ d(f Т 1

as ~~ г аэ ~ 2я г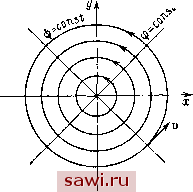

Рис. 21.

Начало координат л=0 (центр окружностей) является особой точкой. Скорость > О при Г > О, т. е. положительному значению циркуляции соответствует движение по окружности против часовой стрелки. Иногда говорят о направлении циркуляции , понимая под этим направление движения жидкости (Г > О - против часовой стрелки, Г < О - по часовой) .

Установим смысл величины Г. Возьмем контур /, охватывающий начало координат, и вычислим циркуляцию скорости у по этому контуру:

yv,ds = <ds = §d<p = \;4de = r.

Таким образом Г - циркуляция скорости по замкнутому контуру, охватывающему начало координат.

Течение, определяемое (5.4), есть течение от вихря. Если вихрь расположен в точке z = а, то комплексный потенциал

(2) = In (г - а).

П р II м е р 6. Рассмотрим течение, вызываемое присутствием в начале координат источника и вихря:

w (г) = 1 + Ш2 = 2я

(5.5)

Течение, описываемое комплексным потенциалом (5.5), называется течением от внхреисточника. Найдем линии тока в этом течении:

q-iV

Ф + н- ==

(In г + /9),

Ф = (1пг + Ге), г1, = (е-Г1пг).

Линии тока г) = const есть линии тока, на которых 0 - const. Обозначим постоянную через Г In с; тогда

Ппг =

= Г In у , г = се

Линии тока - логарифмические спирали. Линии ф = const - также логарифмические спирали, ортогональные к линиям г{) - const. Если вихреисточник расположен в точке а, то

w{z) = \n [z-a).

§ 6. ПОТЕНЦИАЛЬНОЕ ОБТЕКАНИЕ КРУГОВОГО ЦИЛИНДРА ПОТОКОМ ИДЕАЛЬНОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ

Пусть круговой цилиндр радиуса R движется со скоростью и в потоке жидкости, имеющем на бесконечности заданную скорость V, причем скорости U и V перпендикулярны оси цилиндра. Выбрав плоскость (х, у) перпендикулярно образующим цилиндра, получим плоскую задачу о течении жидкости вне круга, движущегося со скоростью и {Dx, и у, 0) в потоке, имеющем на бесконечности скорость V{Vx, Vy,0). Пусть в начальный момент времени ось цилиндра проходит через начало координат (рис. 22).

Так как движение плоское и безвихревое, то существуют комплексный потенциал w{z) и комплексная

Начнем наше рассмотрение с комплексной

скорости. Из физических соображений ясно, что функция v{z) = = Vx - iVy должна быть определена во всех точках плоскости

Рис. 22.

скорость v{z) = -