{х,у) вне круга радиуса R. Она должна быть всюду однозначна, ограничена и принимать на бесконечности заданные значения. Такая функция комплексного переменного может быть разломлена в ряд Лорана по неположительным степеням г:

б(2) = Со+4 + -45-+ (6.1)

Первый член этого ряда легко находится из условия в бесконечно далекой точке

При 2 = оо из (6.1) следует

1х-г, = Со. (6.2)

Подставляя (6.2) в (6.1), имеем

= у (2) у, - гТ + 1 + il. + ... (6.3)

Проинтегрировав ряд (6.3) по 2, получим комплексный потенциал

(2) = (У,-/1/,)2 + с1П2+У . (6.4)

Комплексный потенциал (6.4) обеспечивает выполнение условий на бесконечности при любых значениях постоянных с, С\, ... ..., Сп, ... Эти постоянные надо определить так, чтобы было выполнено условие обтекания цилиндра

Vn Is = и п. (6.5.

Так как движение потенциальное, то п - - В полярных

координатах г, 9 условие (6.5) на поверхности цилиндра г = R запишется в виде

-[ = t/cos.9 + [/j,sine. (6.6)

Для того чтобы найти постоянные, входящие в w[z), удобно перейти в выражении (6.4) к полярным координатам, отделить вещественную и мнимую части ф и г) и, продифференцировав ф

по г, подставить в (6.6). Полученное равенство будет служить для определения с, Ci, .. , с , ...

Искомые коэффициенты будут, вообще говоря, комплексными. Положим

с = ЛЧ-1В, с = Л + гВ , (6.7)

2 = ге (6.8)

п, подставив (6.7) и (6.8) в (6.4), получим

ю{2) = ц> + п) = (I/., - iVy) г (cos е + i sin 6) + (Л + IB) (In л + /9) + + (1 + 7 (cos e - i sin 9) +

n = 2

+ 1! (4 +/5J 4r (cos я9 - ; sin 9). (6.9)

Из (6.9) легко получить выражение для ф и -ф. Выпишем выражение для ф и производной :

Ф = (V r + ) cos 9 + (+ sin 9 + Л In г -

- 56 + J] (if cos 9 + sin п9) ; (6.10)

=(y.- cos9 + (F.-)sin9 + 4-

7;(/l cosn9 + S sinn9). (6.11)

в условие обтека-

Полол<им в (6.11) г = 7? и, подставив

ния (6.6), буде.м иметь ( Vx - ) cos 9 + ( У, ) sin 9 + 4 -

- (Л cos п9 + S sin пв) = Ux cos е + f/y sin 9. (6.12)

Справа и слева в (6.12) стоят ряды Фурье. Сравнивая соответ-ствуюшие коэффициенты, получим

= 0, Vx~=Ux, Vy- = Uy, Л, = В, = 0 (fe = 2,3, ...), откуда

А = 0, A, = (Vx~Ux)R\ Bi = (Vy-Uy)R Л, = В, = 0 (6.13)

(fe = 2, 3, ...).

Коэффициент В остался не определенным. Введем для него обозначение через новую постоянную Г. Положим

В = -. (6.14)

Подставляя (6.13) и (6.14) в (6.9), получаем выражение для комплексного потенциала

Г {Vx - Ux) R + i (V - и и) R w{z) = {Vx-iVy)z + -ln2 + -- V -(6.15)

Вводя обозначения

запишем решение (6.15) в виде

и, + = и.

W (2) = Vz + (У (У) 41 + In Z.

(6.16)

(6.17)

Это общин вид комплексного потенциала обтекания кругового цилиндра. Он представляет сумму тре.х слагаемых, из которых VooZ - комплексный потенциал поступательного потока, второе слагаемое - комплексный потенциал течения от диполя, третье - потенциал течения от точечного вихря. Таким образом, течение около цилиндра можно рассматривать как течение, полученное наложением поступательного потока на поток от диполя и от вихря. Постоянная Г, и.меющая смысл интенсивности вихря, входит в решение как параметр. У

1. Пусть обтекается неподвижный цилиндр. Тогда U = = О и

ш, (2) = Vz+V +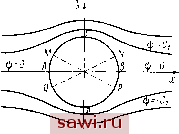

+ i\r\z. (6.18)

Рис. 23.

2. Пусть цилиндр движется в жидкости, покоящейся на бесконечности. Тогда Voc = = Q и

(6.19)

3. Пусть цилиндр ненодвижен ii скорость потока в бесконечности равна нулю. Если t/ = О и ус = Vx = то

(6.20)

И.меем чисто циркуляционное обтекание цилиндра.

Обтекание неподвижного цилиндра. Займемся анализом картины течения около кругового цилиндра. Будем предполагать, что У = О, т. е. цилиндр неподвижен и поток на бесконечности направлен вдоль оси х (ось х всегда можно направить по направлению скорости в бесконечности). Комплексный потенциал (6.18) при Vx = V. V.j = О принимает вид

.Чг) = У(2+4)+41п2.

(6.21)

Рассмотрим два сл\чая.