(6,23)

А. Бесциркуляционное обтекапне цилиндра ] = О (рпс. 23). В атом случае

ф + (-11, = 1/ (.V + ly + /?~ . (6,22)

Отсюда

Линии тока 1] = const, т. е.

есть кривые третьего порядка, симметричные относительно оси у. Линии = С) и = -Cj симметричны относятелыю осп х. Прм ф = О уравнение линии тока распадается па два множителя; у = О - ось X и х + г/ = - окружность.

Рассмотрим ноле вектора скорости. Перейдем к полярны.м коордгтатам (г, В). Тогда

.V==Kcos6(l-), (6.24)

Формулы (6,24) дают компоненты скорости в любой точке потока. Полагая в (6.24) г ~ R, получаем скорость на поверхности цилиндра

= 0, П(5= -2l/3in6. (6.25)

В точках цилиндра вл = тт., 9s = О скорость равна нулю, т. е. точки Л [[ В-критические, В точках 0. =, = --у скорость имеет наибольшую величину, равную 2V. Если скорость известна, нож1ю iiafirn давление из интеграла Бернулли

Ч-С, /j = p(C-2Fsin=e). (6.26)

2 р

Как видно из (6.26), в точка.ч цилиндр;) N, Р, Q,M. определяемых углами ±0, ±(л -0), давление о.-ижаково, и потому главный вектор сил, лсйстиующих и а т1.:ишлр, будет равен нулю.

Б. Обтекание цнлн]1дра потоком с циркуляцией, В этом случае ш(г) имеет вид (6.21). Комплексная скорость

.W = fK(i-l) + i. ,е.2Г,

Найлем ритическпе точк!) потока, в которых :ч = = 0. Приравнивая нулю -й(г)= 1>х - ivy, получаем квадратное уравнение, кории которого г\, Zi дадут координаты критических точек

(6.28)

Здесь возможны различные случаи:

а) -+ 4V-/?-> О - критические точки расположены

Eia обтекаемом цилиндре zi.2 = R симметрично относительно оси у, 1п1 2:[ = 1га 2г, Re г, = -Те г-,. 1

б) -Аг AV-R- -две критические точки сливаются в

Г .

одну, расположенную на мнимой оси: i 2i, = Z = Zo =

п) - + AVJ < О - оба корпя уравнения мнимые, причем [211 </?, \z2\ > R. В области течения имеется одна критическая точка на мнимой оси вне цилиндра.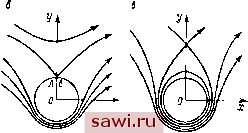

Рнс. 2-1.

Картина течения в рассмотренных случаях, если для определенности принять Г > О, изображена на рис. 24.

В рассматриваемом случае обтекания цилиндра с циркуляцией липни тока симметричны относительно осп у. Давления в точках цилиндра, симметричных относительно оси /;, одинаковы по величине. Си.мметрин течения относительно оси х здесь уже нет. Поэтому возникает сила, действующая на цилиндр в направлении оси /у. Сила в иаиравлении оси х, как и в первом случае, равна пулю.

Результат, зак.1ючающийся п том, что тело, обтекаемое потоком идеальной жидкости, не испытывает сопротивления, носит название парадокса Даламбера.

Если в случае в) величину Г увеличивать так, что WR <

<С, то критическая точка по мнимой оси будет удаляться

от цилиндра и в пределе получим чисто циркуляционное течение.

Можно поставить вопрос: какое же течение реализуется на самом деле? Для идеальной жидкости возможны все указанные случаи. При решении задачи об обтекании цилиндра либо должна быть задана циркуляция, либо какие-то дополнительные условия (например, симметрия потока и др.). Тот факт, что решение задачи содержит произвольный параметр Г, оказывается существенным прн решении многи.х практически важных задач.

§ 7. МЕТОД КОНФОРМНЫ.Х ОТОБРАЖЕНИЙ

Рассмотрим решение задачи об обтекании контура произвольной формы (рис. 25). Плоскость, в которой расположен контур /, выберем за плоскость комплексного переменного z = х 4- iy- Одновременно с плоскостью z рассмотрим плоскость =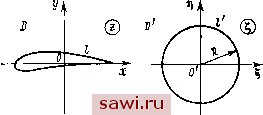

Рис. 25.

= I + IT] И В ней круг радиуса R. Область плоскости z вне контура / обозначим через D, область плоскости вне окружности / радиуса R обозначим через D.

По теореме Римана о конформном отображении существует аналитическая функция 2 = /($), которая преобразует область D в область D таким образом, что точки контура I переходят в точки / и любая наперед заданная точка А D переходит в заданную точку AD. Эта функция будет единственной, если в точке А задан arg/(2;д,) = фд. Воспользуемся этой теоремой, выбрав в качестве точек А и А бесконечно далекие точки плоскостей г и и положим при этом фо = 0. Это значит, что мы берем такую функцию г = / (), которая преобразует бесконечно далекую точку плоскости в бесконечно далекую точку плоскости г и не меняет направлений в этой точке. Для этой функции в бесконечно далекой точке = оо производная

вещественное положительное число, т. е.

есть

= к > 0.