Чтобы преобразоваппс Z. = F{z) переводило внешность отрезка во внешность круга, надо выбрать в (14.4) знак плюс. Таким образом, обратное преобразование имеет вид

C-f- (14.5)

Имея (14.5), можем записать комплексный потенциал обтекания пластинки. Учитывая, что в нашем случае

получим

= -i, /?о = 0, i = f, /? = 1, (14.6)

+ i >(2-V2-a2) + In(2 + V2-a2). (14.7)

Заметим, что формулу (14.7) можно было бы получить непосредственно из формулы (8.9), рассматривая пластинку как предельный случай эллиптического цилиндра, у которого полуось b = 0.

В формулу (14.7) в.ходит циркуляция Г. Для ее определения имеем постулат Чаплыгина-Жуковского. Непосредственное его при.меиение затруднительно, так как у пластинки имеются две острые кромки. Нас интересует пластинка как модель закругленного спереди тонкого профиля с задней острой кромкой. Скорость в задней острой кромке будет конечна, если в соответствии с постулатом Чаплыгина - Жуковского циркуляцию определим по формуле (9.9):

r = 4nkR\v\sm{Qo - a).

Здесь а - угол, образуемый направлением невозмущенного потока с осью х; Во - угол, определяющий положение в плоскости точки А, в которую переходит задняя острая кромка А.

В нашем случае Эо = 0, й = --, R==l, и выражение для

циркуляции будет

r = -2naysina. (14.8)

Соответственно выражение для комплексного потенциала можно записать в виде

+ ia I I sin a\n(z + л/г - a= ). (14.9)

Здесь Voo = Uooe °, Uoo = Уоое . Имея комплексный потенциал, можем найти комплексную скорость у и ее составляющие Vx и Vy в точках пластины. Картина обтекания приведена на рис. 30, а.

Определим силу, действхющЮ на пластику, используя формулу (14.8) для циркуляции. По теореме Жуковского

R = ipvr - - 2л/ра I у р е- sin а.

(14.10)

(14.11)

Откуда

Rx = - 2л;р \v\-a sin- а, Ry = 2лр I \- а sin а cos а.

Интересно отметить следующее. Хотя в идеальной жидкости все элементарные напряже1Н1я нормальны к пластинке, возникает результирующая сила Rx< направленная по касательной к ней. Это связано с те.м, что постулат Чаплыгина - Жуковского накладывает ограничение на величину скорости лишь у задней острой кромки. Если представить себе переднюю кромку закругленной, имеющей малый радиус кривизны, то скорости вблизи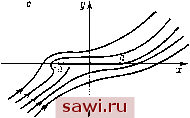

Рис. 30.

носовой части будут очень велики, а давление, согласно уравнению Бернулли, мало. Образующаяся разность давлений между кормовой и носовой частями профиля приводит к появлению некоторой подсасывающей силы, параллельной оси х. Если радиус кривизны закругления устремить к нулю, то скорость вблизи передней кромки будет неограниченно возрастать, а давление - падать. Непосредственными вычислениями можно убедиться, что при этом подсасывающая сила будет стремиться к некоторой предельной величине, совпадающей со значением Rx из (14.11).

Величина силы Жуковского для пластинки

P = \R\ = 2лар I Р sin а. Часто рассматривают коэффициент подъемной силы

Up - -j

(14.12)

(14.13)

В случае плоского течения за S принимают произведение .хорды на единицу размаха крыла. В нашем случае S = 2а и

Ср - 2л sin а.

(14.14)

При малых углах а

Ср2па, -j2n. (14.15)

Ранее была получена формула (13.9) для момента сил, действующих на профиль. Учитывая (14.6), получим выражение для момента сил, действующих на пластинку, в виде

L = -Re(2n/pyP e-<) = -p\vfsin2a. (14.16)

Учитывая (14.12), выражение для L можно записать в виде

L = --cosaP. (14.17)

Из (14.17) след)ет, что точка приложения равнодействующей

силы находится на расстоянии -j части хорды от передней

кромки (рис. 30,б).

Эксперимент показывает, что результаты, полученные при рассмотрении обтекания пластинки, могут быть использованы для тонких профилей при малых углах атаки.

§ 15. ОБТЕКАНИЕ ПРОФИЛЕЙ ЖУКОВСКОГО А. Профили Жуковского

Было установлено, что конформное преобразование

z = {z + j) (15.1)

отображает внешность круга единичного радиуса в плоскости t, во внешность отрезка [-с, с] вещественной оси плоскости 2. Перепишем формулу (15.1) в виде

22 = cg + -J (15.2)

и введем новые переменные z и 1, с помощью преобразования подобия

22 = 2, с? = Г. (15.3)

Тогда получим

2 = r + -f. (15.4)

Преобразование (15.4) переводит внешность круга радиуса с в плоскости во внешность отрезка [-2с, 2с] плоскости z. Перепишем (15.4) следующим образом;

6 Зак, 1031 161