Для однозначности выберем ту ветвь корня, которая обеспечивает его положительное значение при z = х > а. Аналитическая функция f{z) определена во внешности профиля, однозначна и в силу (3.1) стремится к нулю, когда z стремится к бесконечности. Если найдем l(z), то станет известной и искомая

скорость возмущений

Будем искать /(г) во внешности разреза (-~а,а). Пусть Ll - контур, охватывающий отрезок (-а, а), и z - точка вне этого контура. Введем функцию комплексного переменного

Ф(?) =

Jit)

(3.4)

считая 2 параметром. Функция Ф(0 имеет полюс первого порядка в точке t, = Z. Окружим эту точку замкнутым контуром

/ и проведем конгур L2так, чтобы он содержал внутри себя контуры / и Ll. Обозначим через 1 и /?2 разрезы, соединяющие контур / с Ll и L2. Контур L (рнс. 36), состоящий из контуров Ll, /, L2 и разрезов Ru R2, проходимых дважды, ограничивает односвязную область, в которой функция Ф() регулярна. Интеграл от функции, вычисленный по этому контуру, равен нулю: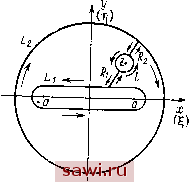

Рис 36.

5Ф(С) = 0. (3.5)

Поскольку интегралы по разрезам, проходимым в противоположных направлениях, в сумме дают нуль, из (3.5) следует, что

\o{t,)dt,+ O{0dZ+\O{0dl==0. (3.6)

Первый интеграл в (3.6) вычислим по формуле Коши

S,-rfS = 2 7(2).

Далее учтем, что равенство (3.6) имеет место при любых контурах Ll и L2. Поэтому выберем в качестве контура L2 окружность большого радиуса R и устремим R к бесконечности. Интеграл по L2 при этом устремится к нулю, так как /()->0 при

? -> ОО-

Таким образом, равенство (3.6) примет вид

2я (г)+ 5 Ф() 4 = 0

fit,)

(3.7)

Рис. 37.

Специализируем теперь вид контура Li. Выберем Li в виде, указанном на рис. 37, и будем стягивать Li к отрезку (-а, а), устремляя е к нулю. Интегралы по окружностям С] и Сг при этом будут стремиться к нулю. В результате получим

Введем компоненты скорости 0(1, т)), vil, п) в подынтегральные выражения в (3.8). Из определения (3.3) для f(0 следует

f{Q = fU + Ш) = [< (1, ц) - ivy il, г,)] V .

Так как на верхнем берегу разреза

/е + Ю-f А /Z±T ,.

УТ -у l + iO-a --

а на нижнем

равенство (3.8) можно переписать в виде

2л УаЛ/ а-1 1-2

Объединим в этом выражении члены с и и члены с v:

il, +0) + у (1, -0) 1-г

, i Г- /T + j- Vyil,+Q) + Vyil, -0)

(3.9)

Учтем теперь граничные условия (3.2) для проекции на ось у скорости возмущений

и примем,что

vM, +0) = ;(£, -о) = у

vil, +0) + <(i, -0) = 0.

(3.10) 181

Подставляя (4.7) в (4.6), получаем

dz л ]-а z-l ]-а dl г-1 Так как 5 (а) = 5 (-а) == О, то

dz л ]~а г - I

Из (4.8) видно, что постулат Чаплыгина - Жуковского выполняется, если задняя кромка профиля z - а - точка возврата (Па) (а) = 0).

§ 5. РЕШЕНИЕ ЗАДАЧИ ОБ ОБТЕКАНИИ ПРОИЗВОЛЬНОГО ТОНКОГО

ПРОФИЛЯ

Л. и. Седовым был предложен метод, позволяющий получить решение задачи обтекания произвольного тонкого профиля, если известно решение двух задач, рассмотренных в § 3 и 4: обтекания профиля без толщины и бесциркуляционного обтекания симметричного тонкого профиля.

Рассмотрим тонкий профиль произвольной формы

УвЛх), Уп = Лх). (5.1)

Образуем профиль без толщины

и симметричный профиль

Очевидно, что

Ув ~~ 2

Ун Ув 2

Ув = у[у[\ у -=у1 + у1.

(5.3)

Требуется найти комплексный потенциал возмущений w{z), заданный во внешности контура (5.1) и удовлетворяющий условиям на бесконечности

L = 0, ,5.4,

на контуре

ypix, +0) = -Ув(х),

ф(х, -0) = -УЛ)

и постулату Чаплыгина - Жуковского.

Пусть функции tc, (z), wniz)- потенциалы возмущений в случае обтекания профилей (5.2) и (5.3) соответственно. Эти