преобразовании правая (левая) система координат переходит в правую (левую), то различия в формулах преобразования тензоров и псевдотензоров нет (А= 1). Поэтому когда в рассмотрении имеют дело только с правой системой координат, псевдотензоры часто называют просто тензорами. Приведем примеры псевдотензоров.

1. Векторное произведение векторов а и b меняет знак на обратный прн переходе от правой системы к левой (и наоборот), т. е. с = аХЬ - псевдотензор первого ранга (псевдовектор).

2. Угловая скорость вращения твердого тела является псевдовектором.

3. Псевдотензор Леви - Чивита - псевдотензор третьего ранга D = = lldkim II. антисимметричный по всем парам индексов и удовлетворяющий условию d[23 = 1 в какой-либо правой системе координат. Все его компоненты, имеющие два одинаковых индекса, равны нулю, н тензор имеет только шесть компонент, у которых все три индекса различны. Составляющие dikl(iфkфl) принимают значение, равное единице, если (, k, I - четная перестановка тройки (I, 2, 3), и равное -1, если i, k, I - перестановка нечетная. Таким образом,

d\23 - 231 = 312 =1. 132 = = 321 = -1-

Во всех правых системах координат псевдотензор Леви -Чивита имеет один и тот же вид.

6. Умножение псевдотензоров и тензоров. Произведение псевдотензора на псевдотензор является тензором (так как = 1). Если А и 5 - псевдотензоры рангов т и п, то А-В - тензор ранга т-\-п. Произведение тензора на псевдотензор является псевдотензором. Если А-тензор ранга т, В - псевдотензор ранга п, то А-В - псевдотензор ранга т -\- п.

Рассмотрим примеры.

1. Возьмем псевдотензор Леви - Чивита D = \\dkim\\ и тензор второго ранга, образованный из векторов а и b (диаду):

С = II Ср, II = 11 арб, 11. Перемножив псевдотензор D на тензор С, получим псевдотензор пятого ранга

T = \\dklmapbq\\.

Выполним два раза операцию свертывания по индексам I п р п индексам т н q. При двухкратном свертывании ранг псевдотензора понизится на четыре и получим псевдотензор первого ранга (псевдовектор R). Положим l = p = i, m. = q = j. Тогда

. = Zl, 21. ЛЛ 1.2.3).

Используя значения dkij, получаем

Ri = 1230263 + 1321362 = 263 - 362, R2 = o-zbi - й\Ьз, Rs = a\b2 - 0261-

Из выражений для проекций видно, что R = а X Ь, т. е. R -векторное произведение векторов а и Ь.

2. Если псевдотензор Леви - Чпвита D умножить на тензор второго да,

где ai - составляющие вектора а, то получим псевдотензор пя-

ранга 24

того ранга. Если этот тензор

dimn \ свернуть диа раза по индексам i н

п и индексам и т, то получим псевдотензор первого ранга. Это будет rota.

7. Примечание. В теории аффинных ортогональных тензоров использовались прямолинейные ортогональные координаты и их преобразование опять в прямолинейные ортогональные координаты. Эти линейные ортогональные преобразования определялись таблицей направляющих косинусов. Можно рассматривать и неортогональные линейные преобразования.

Пусть преобразование координат определяется формулой

Тогда для инвариантной функции ф(г) получим

Эф Y3 dKj ,

дх дх\ ~ Lik=\ dl*

Вообще говоря, матрицы g и g\ не обязательно совпадают (совпадение имеет место для ортогональных преобразований), поэтому законы преобразования компонент градиента скалярной функции и компонент вектора г различны. В связи с этим в общей теории тензоров оказывается необходимым различать два вида векторов и тензоров - контравариантные и ковариант-ные. Не приводя полного определения, дадим часто употребляемое. Говорят, что контравариантный вектор - это такой вектор, компоненты которого Л,- преобразуются при переходе к другой системе координат, как компоненты вектора г. Аналогично величины Ai определяют ковариантный вектор, если при переходе от одной системы координат к другой эти компоненты преобразуются как компоненты градиента функции, т. е. как частные производные по координатам. Для аффинных ортогональных векторов понятия ковариантного и контравариантного векторов являются совпадающими. В общей теории тензоров рассматриваются не только неортогональные, но и нелинейные преобразования координат.

§ 8. СКОРОСТИ И ПЕРЕМЕЩЕНИЯ ТОЧЕК БЕСКОНЕЧНО МАЛОГО ОБЪЕМА СПЛОШНОЙ СРЕДЫ

Пусть в пространстве, связанном с системой координат х, у, Z, движется жидкость. Рассмотрим некоторую малую частицу жидкости с объемом т в момент времени t. Выберем в этом объеме некоторую точку А и примем ее за полюс (рис. 1). Обозначим ее радиус-вектор через Го- Выберем в этом же объеме другую точку В и обозначим ее радиус-вектор через г. Относительный радиус-вектор АВ обозначим через р, его проекции -

через I, ц, t,. Если координаты точки А обозначить через х, у, г, то координаты точки В будут х-\- I, у + ц, г + ь-

Рассмотрим ту же массу жидкости в момент t4-dt. Точки А и В займут новое положение А и В. Радиус-векторы, соответствующие новому положению точек, обозначим через г, г, р. Очевидно, что

Р = г-Го, р==г-г; (8.1)

Вектор dp = р - р с проекциями dl, dx], dt, характеризует изменение относительного положения точки В по отношению к точке А за время dt. С учетом (8.1)

dp = р р = (г - г) - (г - г ) = (г - г) - (г; - г ). (8.2)

Если через v.4 и vb обозначить скорости точек Л и В, то Гц - Гц = Л - перемещение точки Л, г- г = Vg Л - перемещение точки В за время dt. Поэтому (8.2) можно записать в виде

р = (Уд-Ул)Л. (8.3)

Здесь

Vb = V (г) = V (х+г, у+ц, Z+0, = V (го) = V (х, у, г).

(8.4)

Считая рассматриваемый объем т малым, разложим

Рис.1. функцию v(.-f I, г/+ Ti,z--S)

в окрестности точки х, у, г в ряд Тейлора. С точностью до величин второго порядка малости получим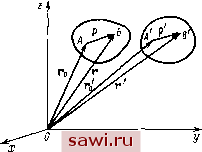

dp =

.дх ду В проекциях на оси координат

, dv , дч (.Т

(8.5)

L дх

1 + 1 +

dx dy dz

dvu dv

Z dt, dt, dt.

(8.50

Чтобы выяснить характер относительного изменения положений точек Л и В, преобразуем равенства (8.5). Сделаем это