зом, интеграл по любому объему т, содержащему начало координат, равен одному и тому же значению q. Вследствие этого подынтегральная функция Аф может быть представлена в виде

Аф = qb (г),

где 8(г) = 8{х)8(у)8{г)-трехмерная дельта-функция, или функция Дирака, равная нулю всюду, кроме г = О, такая, что

На основании этого можно считать, что в области, содержащей начало координат, потенциал ф = -удовлетворяет не

уравнению Лапласа, а уравнению Пуассона с правой частью, содержащей функцию Дирака.

Хотя приведенное определение дельта-функции, как легко видеть, математически противоречиво, формальное использование этой функции часто оказывается очень полезным. В современной математической физике построена строгая теория функций Дирака и других аналогичных функций (теория обобщенных функций).

§ 2. ДИПОЛЬ В ПРОСТРАНСТВЕ

Рассмотрим течение от источника и стока. Пусть источник и сток расположены на расстоянии / друг от друга и имеют обильности, одинаковые по величине и противоположные по знаку. Пзсть система координат выбрана так, что они расположены на оси Z в точках 1/2 и -1/2. Так как уравнение для ф линейно, то

Ф = ф1 + ф2, (2.1)

где ф1 - потенциал течения от источника:

Р = - -г vftFTtW -

ф2 - потенциал течения от стока:

+ -Ь (2 tlW

Подставим (2.2), (2.3) в (2.1). Получим

д Г 1 1 )

4л \ л: + г/2 + (г - Щ) М7ЧЧГ+772р J

Рассмотрим предельный случай, когда q->oo, /->0, причем ql = М = const. В этом случае течение называется течением от пространственного диполя. Разложим выражение в квадратных

скобках в ряд Тейлора по степеням / и перейдем к пределу при /->0.

В результате получим

~ где М = (?/ = const.

(2.4)

Величина М называется моментом диполя. Нетрудно видеть, что (2.4) можно записать в виде

Если ось диполя 1 не совпадает с координатной осью, то потенциал течения от диполя имеет вид

М д

4я dl

= cos (/, + cos (/, г/) + cos (/, z)

dl дх ди дг

- производная по направлению оси диполя

§ 3. ОБТЕКАНИЕ СФЕРЫ

Рассмотрим сферу радиуса R, двиисущуюся со скоростью и вдоль оси z; вектор скорости набегающего потока V направлен по оси Z.

Требуется найти потенциал скоростей ф, удовлетворяющий уравнению Лапласа

Лф = 0

и граничным условиям на поверхности сферы

и на бесконечности

= 0,

дф ду

= 0,

(3.1) (3.2) (3.3)

Записывая уравнения Лапласа в сферических координатах и учитывая, что течение осесимметрично и ф не зависит от X, получаем для функции ф = ф(г, 9) следующее уравнение:

(-)+ir(- t)=<-

дг л, I I лй v лй ) (3.4)

!раничные условия (3.2), (3.3) можно записать в виде (рис.39)

= cos0; (3.5)

trU., 1 cos 0, eU = -Fsin9, t;,U = 0, (3.6)

Fcos е,

= - l/sinG.

(3.7)

Исходя из вида уравнения (3.4) и граничных условий (3.5), (3.7), решение будем искать в виде

Ф(г, e) = Q(r)cose. (3.8)

Подставляя (3.8) в (3.4), приходим к обыкновенному дифференциальному уравнению Эйлера для функции Q(r)

+ 2r4--2Q = 0.

(3.9)

Представив решение в виде Q = г , получим следующее уравнение для к:

2 + 2 = О,

корни которого ki = -2, 2=1-Поэтому

Q = C,r +

Ф=(с,г + -) cose.

(3.10)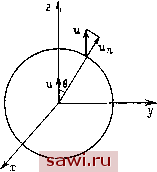

Постоянные Ci и Сг определим из граничных условий. Из (3.10) имеем

Ог U = Ci cos 9,

вU = -ClSine, t,J = 0.

(3.11)

Сопоставляя (3.11) и (3.6), видим, что Ci = V. На поверхности

Рис. 39.

шара

Сравнивая (3.12) и (3.5), получаем

Таким образом, потенциал скоростей имеет вид

Ф(г, e) = (v, + XziiL)cose.

Можно переписать эту формулу в виде

(3.12) (3.13)

(3.14)

(3.15) 191