ГЛАВА XV

ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА В ЖИДКОСТИ

§ J. ОБЩИЙ ВИД ПОТЕНЦИАЛА СКОРОСТЕЙ

Пусть в жидкости движется некоторое твердое тело, ограниченное гладкой поверхностью S. Отнесем это движение к некоторой неподвижной системе координат XoyoZo и предположим, что скорость поступательного движения рассматриваемого тела относительно взятой системы отсчета равна Uo (рис. 42). Предположим также, что мгновенная угловая скорость тела относительно выбранного нами в теле полюса О равна ю. Тогда скорость произвольной точки N, принадлежащей этому телу в его движении относительно системы XoyoZo, будет выражаться формулой

U = Uo + (ю X г) = Uo + Uo

где г - радиус-вектор, проведенный из полюса в точку N. Будем далее считать, что жидкость до того момента времени, когда тело начало в ней двигаться, находилась в покое. Движущееся тело будет возмущать окружающую его жидкость, создавая в ней поле скоростей v{t,XQ,yo,Zo). Будем предполагать, что скорости возмущенного движения жидкости убывают при удалении от тела и на бесконечности жидкость покоится. Если жидкость идеальна, баротропна и массовые силы имеют потенциал, то возмущенное движение жидкости будет также потенциальным. В слу- Рис. 42.

чае несжимаемой жидкости потенциал этого движения будет удовлетворять уравнению Лапласа

Аф = 0. (1.1)

Вследствие непроницаемости тела на его поверхности в каждой 1тОчке должно выполняться граничное условие

где п - орт нормали.

Для удобства вычислений рационально в дальнейщем воспользоваться подвижной системой координат х, у, z с началом в полюсе О, неизменно связанной с движущимся телом. Если закон движения тела известен, то для каждого заданного момента времени t координаты xq, уо, Zo можно выразить через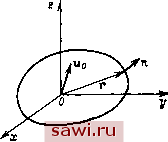

координаты X, у, z м представить потенциал (t, Хо, у, Zo) как функцию X, у, z:

4>{t, хо, уо, Zo)(fit, X, у, z). (1.3)

Переход от системы Хо, уо, Zo к системе х, у, z совершается с помощью переноса начала и поворота системы координат. Как известно, при указанных преобразованиях координат уравнение Лапласа сохраняет свой вид, так что

Acf((, X, у, z) = 0. (1.4)

Условие на бесконечности также сохраняет свой вид, так как соотношения (х + + 25) -> оо и (х -]- г/2 -]- г) оо равносильны (в течение любого промежутка времени тело пройдет лишь конечный путь). Условие иа теле значительно упростится, поскольку оно будет записано в системе координат, жестко связанной с телом, и будет иметь вид

== {uox + Ишх) а + {чоу + у) Р + (uoz + Чш) У, где а = cos (га, х), р = cos (га, у), у = cos (га, 2),

И(ох == (i>yZ - ЩУ, иу = &zX - &xZ, = хУ - уХ,

т. е.

= що. + ИойР + ozY + (t/Y - 2р) + (Ну (2а - ху) +

+ щ{х-уа). (1.5)

Из формулы (1.5) непосредственно можно заключить, что потенциал ф должен линейно зависеть от скоростей, изменяющихся во времени, и будет иметь структуру

ф {t, X, у, Z) = ИохФ! + 0 ф2 + ИоФз + Ю.хФ4 + г/Фб + гФб. (1 -6)

где функции ф; ((=1, 2, 6) будут функциями координат X, у, 2. Такая форма представления потенциала принадлежит Г. Кирхгофу.

Из изложенного видно, что если заданы форма тела и закон его движения, то определение потенциала возмущенного движения приводит к задаче: найти вне поверхности 5 гармоническую функцию, стремящуюся к нулю на бесконечности, нормальная производная которой на S принимает согласно (1.2) заданные значения (1.5). Эта задача в теории потенциала носит название внешней задачи Неймана.

Вследствие линейности (1.6) все функции ф,-(д;, г/, г), каждая в отдельности, должны удовлетворять уравнению Лапласа

Дф. = 0 (г=1, 2, .... 6), (1.7)

условиям на поверхности 5

Определение каждой из этих функций приводит, следовательно, к задаче Неймана.

Из (1.8) видно, что функция ф1 соответствует тому случаю движения тела, когда

Иох = 1. иоу==Щг = 0, щ = (ау = а = 0, (1.10)

т. е. тело движется в направлении оси х с единичной скоростью. Аналогичное значение имеют функции фг и фз. Функция ф4 соответствует случаю, когда

UQx = Uoy = UQ, = 0, а>х = \, C0j, = o = 0, (1.11)

т. е. тело вращается с единичной угловой скоростью вокруг оси X.

Общий вид потенциала (1.6) определяет зависимость ф от времени для нестационарных задач. Из (1.6) видно, что функция ф зависит от времени только через посредство Uq и ю, по-Эф.

зависят лишь от координат точек по-

скольку функции верхности тела.

§ 2. ПОВЕДЕНИЕ ПОТЕНЦИАЛА СКОРОСТЕЙ В ОКРЕСТНОСТИ БЕСКОНЕЧНО УДАЛЕННОЙ ТОЧКИ

Замечание о сферических функциях, рим уравнение Лапласа

ди . Эц , ди

+ -t- - - и.

Рассмот-

Построим решение этого уравнения, имеющее вид однородных полиномов степени п. При п = О существует одно линейно-независимое решение щ = а = const. Однородный полином первой степени U = ах-\-by-\-cz содержит три линейно-независимых решения. Квадратичный полином общего вида г = ах-\- Ьу -\-+ cz + dxy -\- eyz -j- fzx будет удовлетворять уравнению Лапласа, если а + & + с = 0. Таким образом, при п = 2 будем иметь пять линейно-независимых решений.

Можно показать, что существует 2п + 1 линейно-независимых однородных полиномов степени п, удовлетворяющих уравнению Лапласа.