в момент времени t будем характеризовать моментом времени t и положением Мо частицы на кривой AqBq в начальный момент времени /о (рис. 43).

Положение частицы на AqBq можно задавать длиной дуги S, отсчитываемой от точки Aq. Если г - радиус-вектор точки М, то г = r(s, /), а скорость v и ускорение w согласно определению будут равны соответственно

v = f. w = . (1.3)

Так как при интегрировании вдоль контура время t фиксировано и dr = ds, то (1.1) можно переписать в виде

rW=Slv.-ffds. (1.4)

Здесь / - длина дуги AqBq. В интеграле (1.4) пределы интегри-рования постоянны, и при отыскании можно проводить дифференцирование под знаком интеграла:

г (дм дт , дг \ , C dr , , C dv ,

Вдоль контура ds = dr, v j-rfs =(-j-) = d Переходя к старым переменным, получаем

dT ГВ ГВ {ГВ vi Ол

Если кривая замкнута {А = В), то

= (bwdr. (1.6)

Таким образом, производная по времени от циркуляции скорости по замкнутому (жидкому) контуру равна циркуляции ускорения по тому же контуру.

Применим полученный нами результат для доказательства так называемой теоремы Томсона: если жидкость идеальна, баротропна и массовые силы имеют потенциал, то циркуляция скорости по любому замкнутому жидкому контуру не зависит от времени.

Для идеальной жидкости имеем

w=:-lgradp + F. (1.7)

Так как жидкость баротропна (р = р(р)), то существует функция Р{р) такая, что grad р = grad Р. Вследствие того, что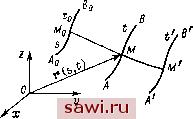

массовые силы консервативны, F = -grad V. Поэтому, учитывая условия теоремы Томсона, будем иметь

w = -grad(P+У). (1.8)

Подставив (1.8) в доказанное равенство (1.6), получим

= - § grad (Р+ К) dr = - § d(P + Ю = 0, (1.9)

откуда

Г (О = const.

Таким образом, циркуляция скорости по любому замкнутому контуру, движущемуся вместе с жидкостью, остается для этого , контура постоянной во все время движения.

Замечание. При записи (1.9) учитывается, что интеграл вычисляется для данного момента времени, поэтому grad/.dr = = df.

Поскольку из теоремы Стокса следует, что поток вихря через поверхность 5 равен циркуляции скорости по контуру, ограничи- Рис 43.

Бающему эту поверхность, то из

теоремы Томсона вытекает, что поток вектора вихря через поверхность S, ограниченную жидким контуром, не зависит от времени.

§ 2. ТЕОРЕМА ЛАГРАНЖА

Пусть выполнены условия теоремы Томсона, т. е. жидкость идеальна, баротропна и массовые силы консервативны. Тогда справедлива следующая теорема Лагранжа: если в некоторый момент времени в фиксированной массе жидкости нет вихрей, то их не было в предыдущие и не будет в последующие моменты времени.

Действительно, пусть в рассматриваемой массе жидкости, находящейся в объеме т, в момент времени нет вихрей, т. е. Q=0. Тогда течение жидкости потенциально: v = grad ф и циркуляция скорости Го по произвольному замкнутому контуру /о равна нулю:

Гo = (v dr==(gradф dr = 0. (2.1)

Рассмотрим выделенную массу жидкости в любой другой момент времени t и в ней возьмем произвольный контур /. Любому контуру / в момент t можно сопоставить контур /о в момент 0. состоящий из тех же частиц жидкости, для которого справедлива формула (2.1).

По теореме Томсона циркуляция Г по контуру / будет также равна нулю. Применяя формулу Стокса, получаем для любого момента времени

55Q d5 = r = 0, (2.2)

где 5 - поверхность, ограниченная контуром / и целиком находящаяся в объеме, занимаемом жидкостью.

Поскольку для любой области S интеграл равен нулю, из (2.2) следует, чтоО = 0. Теорема Лагранжа составляет основу для рассмотрения безвихревых течений в гидромеханике идеальной жидкости, так как если движение жидкости безвихревое (потенциальное) в начальный момент времени, то оно будет безвихревым (потенциальным) и в последующие моменты времени.

Все предположения в теореме Лагранжа существенны. В частности, существенно не сформулированное явно предположение о гладкости поля скоростей.

В условиях Земли теорема Лагранжа является приближенной, так как массовые силы будут консервативны, если не учитывать силы Кориолиса, а сжимаемую жидкость можно рассматривать как баротропную, если пренебречь рядом факторов, например, теплопроводностью и др.

§ 3. ТЕОРЕМЫ ГЕЛЬМГОЛЬЦА

В этом параграфе предполагаются выполненными условия теоремы Томсона, а именно: жидкость идеальна, баротропна и массовые силы консервативны.

Первая теорема. Если жидкие частицы в какой-либо момент времени образуют вихревую линию, то эти же частицы образуют вихревую линию во все последущие и все предыдущие моменты времени.

Докажем сначала, что если в некоторый момент времени жидкие частицы образут вихревую поверхность, то эти же частицы образуют вихревую поверхность при всех t {t <.to и

t>to).

В каждой точке вихревой поверхности согласно ее определению вектор вихря скорости перпендикулярен нормали к поверхности, т. е.

Q = Q-n = 0. (3.1)

Пусть жидкие частицы в момент to образуют вихревую поверхность 5о. Рассмотрим на этой поверхности произвольный замкнутый контур /о, ограничивающий участок поверхности Оо. Согласно формуле Стокса имеем

Г = V dr = 5 J П . п dS = 0. (3.2)