тельно удовлетворяет этому равенству. Рассмотрим сначала выражение А div А. Учитывая (6.17), получим

А div А = div АА = - div й = - div rot v = 0.

Таким образом, div А - гармоническая функция. Нетрудно проверить, что

lim div А = 0.

Г->оо

Но известно, что функция, гармоническая во всем пространстве и стремящаяся к нулю на бесконечности, есть тождественный нуль. Следовательно, div А = 0.

2. Установим единственность полученного решения задачи (6.1), (6.2), (6.6). Предположим, что наряду с построенным решением V имеется другое решение задачи vi. Тогда разность U = V - Vi удовлетворяет условиям

divu = 0, rotu = 0, uL = 0.

Покажем, что и = 0. Очевидно, что и - потенциальное поле U = grad ф. Но div и = div grad ф = 0. Следовательно, ф, а вместе с ней и U являются гармоническими функциями. Таким образом, U - гармоническая функция, обращающаяся в нуль на бесконечности. Отсюда следует, что и = О и Vi s у. Единственность полученного нами решения доказана.

Замечание. Скажем несколько слов о решении в области т, ограниченной поверхностью S, задачи (6. ), (6.2) с граничным условием (6.4). Решение этой задачи можно искать в виде

V = grad ф + rot А -f U,

где ф и А - построенные выше функции, а и удовлетворяет уравнениям div и = О, rot и = 0. Очевидно, что и = grad ijj. Тчзгда div u = div grad ij; - Аф = 0. Для нормальной составляющей Vn будем иметь

г д<р

+ TOtnA\s + Un\s=Vn{M).

Следовательно,

. = f{M), (6.21)

где f (М) - Уп{Щ - - rot А Is. Поскольку f - заданная функция, для a3 получаем задачу Неймана.

§ 7. СКОРОСТИ, ИНДУЦИРУЕМЫЕ ВИХРЕВОЙ НИТЬЮ

Пусть в жидкости, заполняющей все пространство, имеете , замкнутая вихревая трубка с конечным объемом т. Поле скоростей, индуцируемое такой вихревой трубкой, определяется формулой (6.20). В нашем случае il{x,y,z)- О вне области т. Так

как мы предполагаем, что в жидкости нет источников, то Q{x,y,z)= О всюду. Поэтому

Пусть а - сечение трубки, / - средняя линия трубки, at - единичный вектор касательной к средней линии. Полагая вихрь скорости Q постоянным в каждом сечении трубки, для элемента вихревой трубки длины dl можно записать ildx - iladl = = tQadl. Тогда

I a I

Устремляя a к нулю (при этом Q- оо), но так, чтобы произведение Qcr оставалось постоянным, получаем вихревую нить с интенсивностью Г = Qa. По теореме Гельмгольца интенсивность Г постоянна вдоль /, поэтому, переходя к пределу, получаем

=°*5>/. (7.3)

Проекции скорости v на координатные оси определяются по формулам

Вектор t не зависит от координат х, у, г. Выполняя дифференцирование под знаком интеграла и учитывая, что grad- =

- , где г = (л; - I) i + (/ - Tl) j + (2 - Й к. получаем

у =

в скобках под знаком интегралов в (7.4) стоят компоненты векторного произведения двух векторов t и т = . Поэтому

формулы (7.4) для скорости, индуцируемой в пространстве вихревой нитью, можно записать в виде

Очевидно, что элемент вихревой нити А/ порождает в точке М (г) скорость Av:

*v = l(tXf)i- (7.6)

С численным значением Ау = sin а--. Здесь (х -угол

между векторами t и г (рис. 46).

Формулы (7.5) и (7.6) аналогичны формулам Био -Савара в электродинамике.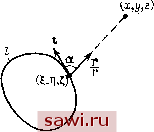

Рис. 46.

Рис. 47.

§ 8. ПРЯМОЛИНЕЙНАЯ ВИХРЕВАЯ НИТЬ

Формулы (7.5), (7.6) были выведены для замкнутой вихревой нити, однако они имеют смысл и для бесконечной вихревой нити. В качестве примера рассмотрим прямолинейную вихревую нить, проходящую через точку (, т)) параллельно оси z (рис. 47). Тогда tx = ty = О, tz=l, dl = dt, и формула (7.5) приобретает вид

Hj.Hi в проекции на оси координат

Г , . Г+°° dt,

Vx==-{y\~y)] -.

v, = 0.

(8.2)