Таким образом, сделанные предположения не обеспечивают возможности выполнения постулата Чаплыгина - Жуковского. Нужно отказаться от некоторы.х из них.

Предполагая, как и раньше, что двиление идеальной жидкости установившееся и потенцпалыюе, не будем требовать, чтобы Vx, Vy, Vz всюду вне крыла былп непрерывны. Поскольку мы хотим сохранить постулат, т. е. чтобы жидкость, обтекая крыло конечного размаха, покидала его в задней острой кромке, и так как ниоткуда не следует, что скорости частиц жидкости, сходящие с верхней и нижней сторон крыла, одинаковы, то естественно допустить, что в жидкости имеется поверхность S, проходящая через заднюю острую кромку, на которой нет непрерывности скоростей. Так как движение установившееся, то эта поверхность Е должна быть неподвил<на в пространстве. В точках этой поверхности с верхней и нижней сторон должны быть выполнены условия непрерывности давления и нормальной составляющей скорости, т. е.

(1.4)

При отсутствии массовых сил из интеграла Бернулли

v I р

2 + = const следует, что квадрат скорости, а следовательно, и величина скорости непрерывны при переходе через Е. Но = у2 -f v\, где = - нормальная, vx - касательная составляющие скорости. Так как функция непрерывна при переходе через Е, то непрерывна и v\, а тогда и абсолютная величина Vx. Но сама касательная составляющая Vx может терпеть разрыв, при этом при стационарном движении разрыв испытывает только Vz - поперечная составляющая Vx.

Поверхность, на которой терпит разрыв касательная составляющая скорости, может быть интерпретирована как вихрево!! слой. Заметим, что поверхность Е, вообще говоря, неизвестна и должна быть найдена в процессе решения задачи.

Таким образом, задача сводится к отысканию функции qi(x,y,z), удовлетворяющей уравнению Лапласа (1.1), граничным условиям (1.2) на поверхности крыла S, условиям (1.4) на неизвестной поверхности разрыва Е (эти условия нелинейные,

так как давление вырал<ается через ~(f) ( f) + ( fj ) ) условиям на бесконечности. Условия на бесконечности теперь следует формулировать несколько иначе, а именно; Vx - Vno, Vy = 0, Vz = О бесконечно далеко от S и Е.

Основные предположения, которые лел<;ат в основе теории, излагаемой в этой главе, следующие:

1) рассматриваемое крыло тонкое,

2) крыло имеет большое удлинение,

3) применима гипотеза плоских сечений,

4) справедлива схема жидкого крыла.

Выберем оси координат так, чтобы ось х была параллельна скорости Voo невозмущеннсго потока, ось z направлена по размаху крыла. Начало координат поместим в середине размаха крыла.

1) Первое предположенпе означает, что профиль, полученный в сечении крыла плоскостью z = const, тонкий и хорда профиля образует малый угол с направлением скорости (угол атаки а мал).

2) Для крыла произвольной формы в плане за удлинение принимают отношение Я, = где L - размах крыла, S - его площадь в плане. Для прямоугольного крыла S = bL, где b -

хорда профиля и удлинение - s ~ 1)--отношение размаха

к хорде. По второму предположению X велико (практически до-статочно брать Х>А), т. е. крыло длинное и узкое.

3) Гипотеза плоских сечений, оправданием которой служит второе предположение, позволяет в плоскости z = const скорости и давления

Vx = Vx (Х, у), Vy = Vy (х, у), р = р (х, у)

построить так же, как в случае крыла бесконечного размаха.

4) Гипотеза о справедливости схемы жидкого крыла предполагает возможность подобрать такую систему особенностей, которая может заменить действие твердого непроницаемого крыла На поток и вызвать такое же движение жидкости, которое вызывалось действием крыла.

§ 2. ВИХРЕВАЯ СИСТЕМА КРЫЛА И ОСНОВНЫЕ ФОРМУЛЫ

Составим представление об общей схеме рассмотрения задачи с учетом сделанных предположений. Жидкость, заполняющая безграничное пространство, обтекает крыло конечного размаха (рис. 49). С задней острой кромки крыла сбегает поверхность S разрыва касательных составляющих скорости, которую можно трактовать как вихревую поверх?юсть, образованную вихревыми трубками. Выделим на этой поверхности бесконечно тонкую вихревую трубку. При сделанных предположениях (движение установившееся, жидкость несжимаемая, массовые силы отсутствуют) справедлива теорема Гельмгольца, согласно которой вихревые трубки при движении все время остаются вихревыми трубками, перемещаясь вместе с жидкостью. Но поскольку движение уста[10вившееся, это возможно, только если вихревые линии будут совпадать с линиями тока.

Так как крыло тонкое, то можно скорости представить в виде

v = v, где и., vj, - скорости возму-

у, =

ш.еннй, возникающие из-за наличия крыла. Так как последние невелики по сравнению со скоростью Ооо, то линии тока будут мало отклоняться от линий тока невозмущенного движения. Поверхность тока, сбегающая с задней острой кромки крыла, и совпадающая с ней вихревая поверхность будут мало отклоняться от плоскости (x,z). Поэтому приближенно можно принять, что вихревая поверхность совпадает с частью плоскости (X, z), а вихревые линии, образующие эту поверхность, будут прямыми, параллельными оси х.

По теореме Гельмгольца вихревая трубка сохраняет свою интенсивность по всей длине и потому не может оканчиваться в жидкости. Согласно схеме жидкого крыла можно считать все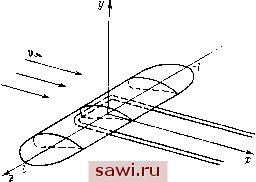

Рис. 49.

пространство заполненным жидкостью. Поэтому вихревую трубку нужно представить продолженной в области внутрь крыла и затем выходящей из него, т. е. каждый вихрь можно представить в виде П-образного вихря. Часть вихря, связанную с крылом, называют присоединенным вихрем, части вихря, покидающие крыло и уходящие в бесконечность, называют свободными вихрями.

Так как крыло имеет большое удлинение (узкое), то все присоединенные вихри рассматривают как один линейный вихрь внутри крыла, расположенный вдоль отрезка оси z (-/ = 2 /), имеющий переменную интенсивность Г = Г(г) вдоль своей длины. От этого присоединенного вихря сбегают свободные вихри, образующие вихревую пелену 2 (рис. 50). Заметим, что в случае крыла бесконечного размаха свободные вихри отсутствуют.

Свободные вихри индуцируют в пространстве скорости. В разных точках пространства эти скорости v/, называемые индуктив-