ными, различны. Но пас интересует течение вблизи крыла. На основании гипотезы плоских сечений можем свести пространственную задачу к плоской. В сечении z = const (-/ < г <5 /) будем рассматривать обтекание профиля потоком, скорость которого складывается из скорости Voo невозмущенного потока и скорости V,-, вызываемой свободными вихрями.

Так как крыло имеет большое удлинение, то на протяжении длины хорды изменения скорости у,- в зависимости от х и вблизи профиля малы. Поэтому можно приближенно принять индуктивную скорость постоянной и равной скорости, вызываемой системой свободных вихрей, в точке на оси 2, т. е. там, где расположен присоединенный вихрь (рис. 51).

Теперь в сечении г = const будем иметь плоскую задачу

обтекания профиля потоком, имеющим скорость Vm = Voo + V;,

где Vi = const = v,(2). Угол а,- между Vm и Voo называют углом скоса потока.

a Рис. 50.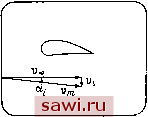

Рис. 51.

Таким образом, вместо пространственного течения около крыла будем рассматривать в каждом сечении z == const плоское обтекание профиля потоком, скорость которого v, зависит от Z.

Итак, задача обтекания крыла конечного размаха разделилась на две - задачу обтекания профиля поступательным потоком и определение изменения циркуляции Г (г) по размаху крыла.

Будем сначала считать Г (г) известной и получим формулы для индуктивной скорости, угла скоса потока, индуктивного сопротивления и подъемной силы.

Выделим элемент крыла шириной dz и подсчитаем силу, действующую на него. По теореме Жуковского эта сила перпендикулярна скорости Vm и рзвна

dR==Qvj:{z)dz. (2.1)

Эту силу можно разделить на две составляющие: подъемную силу

dRy = dR cos ai

и силу dRx, связанную со скосом потока и называемую силой индуктивного сопротивления:

dRx = dR sina;.

Учитывая малость угла а,-, имеем

dRy dR, dRx а; dR. (2.2)

Кроме того, из рис. 51 видно, что tgai =---, а для малых

аг = --. (2.3)

Интегрируя равенства (2.2) по размаху крыла с учетом (2.1), получим формулы для подъемной силы и силы индуктивного сопротивления, действующих на крыло:

Ry = pv Tdz. (2.4)

RxpvuiV dz, (2.5)

lx=-9 ViVdz. (2.6)

Этими формулами определяется силовое воздействие потока па крыло, если известно распределение циркуляции Г (г) по размаху крыла. Преобразуем эти формулы.

От элемента dQ, взятого около точки g присоединенного вихря, отходит свободный вихрь. Интенсивность свободного вихря dV равна изменению интенсивности присоединенного

вихря, т. е. dr = dt,. Бесконечная вихревая нить, параллельная оси X и про.ходящая через точку (О, О, Q, вызывает

Г 1

в точке (.г. О, 2) скорость Vy = - - - g Свободный внхрь питенснвности dT, выходящий из точки t, осп z (полубесконечны!! вихрь), индуцирует в точке оси z скорость

d - iriV (2.7)

Интегрируя (2.7) по размаху крыла (- /, -\-1), получаем скоросп , индуцируемую в точке (О, О, z) системой свободных вихрен;

1 Г

dl z-l-

(2.8)

(При этом интеграл вычисляется в смысле главного значения Кощи.)

Подставляя (2.8) в (2.3), получаем

dr dt

И затем

а 1 Г (29)

toco ]-i dl г-S У-

Удобно в формулах (2.4), (2.9), (2.10) ввести новую независимую переменную, положив 2-= - / cos В (соответственно t,- = -/cosB), и представить Г в виде тригонометрического ряда

Г(е) = 4иЕГ=Н зп 9 (0<е, 0<я). (2.11)

Рассмотрим сначала выражение для подъемной силы. Подставим (2.11) в (2.4):

Ry = pvl {21}-Y,n JsinnOsineffe. (2.12)

( л Гл/2, rn = n,

Учитывая, что sin 9 sin тЭ d6 = < тфп У

/?, = яр(2/)2Ль (2.13)

т. е. подъемная сила определяется только коэффициентом Л, в разложении Г в ряд по синусам.

Теперь запишем выражение для v,. Подставим (2.11) в (2.8). Принимая во внимание, что

f = 1(1) = 4./ Y пАп cos 0 j, (2.14)

получи.м

Vi =--> Л \--Д. (2.15)

л L-in Jo cos 9 - cos 9

Так как

f cos/i6 de sin nQ ,r, ,c\

]o cos9-cos6 = hrr (-l)

TO окончательно для индуктивной скорости будем иметь

sin /(9

Угол скоса потока прн этом выразится (})ормулой

Выралсепие для силы сопротивления получим, подставив (2.11) в (2.5):

Rx = np{2lfJ]jiAl (2.19)