Из (2.19) видно, что при заданной подъемной силе (последняя определяется только через Ai) индуктивное сопротивление будет ыпипмальпым, если все Л, = 0, / 2.

Определим коэффициент подъемной силы и коэффициент индуктивного сопротивления:

Здесь S - площадь крыла в плане.

Используя формулы (2.13) и (2.19) для Ry и Rx, получаем

С, = я-Ль 2

Так как (2/)/S = К - удлинение крыла, то выражения для Су и можно записать в виде

Су = лЯЛ (2.20)

CiniZnmAl. (2.21)

§ 3. КРЫЛО с ЭЛЛИПТИЧЕСКИМ РАСПРЕДЕЛЕНИЕМ ЦИРКУЛЯЦИИ

Рассмотрим некоторые свойства крыла с минимальным индуктивным сопротивлением при заданной подъемной силе. Как было показано выше, у такого крыла подъемная сила и индуктивное сопротивление определяются формулами

?, = яp-(2)Л?, (3.1)

Ry-np{2irAi. (3.2)

Учитывая, что Л, = О, при всех / 2 из (2.11) имеем

г(е) = 4ол,з!пе. (3.3)

Исключив sin 6 из (3.3), с помощью равенства г = -/cos 0 получим уравнение для Г(г)

Из этого уравнения видно, что крыло с минимальным индуктивным сопротивлением при заданной подъемной силе имеет эллип-

тическое распределение циркуляции по размаху. Уравнение (3.4) можно записать в виде

где Yry, = AvAil.

Из формул (2.17) и (2.18) следует, что у такого крыла

Vi = - vAu а,= Л,.

Подъемная сила, индуктивное сопротивление, индуктивная скорость и угол скоса потока определяются только коэффициентом Л].

Крыло с постоянным по раз.маху геометрическим углом атаки а называется геометрически незакручеиным. Крыло с постоянным по размаху эффективным углом атаки = сб - а,- называется аэродинамически незакручеиным. В противном случае говорят, что крыло имеет крутку (соответственно геометрическую или аэродинамическую). Очевидно, что если крыло с эллиптическим распределением циркуляции является геометрически незакручеиным, то оно является и аэродинамически незакручеиным.

Посмотрим, какую форму в плане имеет такое крыло. Запишем два выражения, определяющие подъемную силу, действующую на элемент крыла dz:

dRy = pvV{z)dz,

dRy = CyPb{z)dz.

Приравнивая правые части, получаем

r(z) = Cyb{z).

Поскольку в плоскости (Г, г) мы имеем эллипс, то и b{z) имеет вид эллипса, т. е. рассматриваемое крыло с эллиптическим распределением циркуляции имеет эллиптическую форму в плане. При небольших углах атаки можно приближенно положить Су = А + Вае,

где А, В - некоторые характеристики профиля, ае = а - ai.

§ 4. ПАРАБОЛА ИНДУКТИВНОГО СОПРОТИВЛЕНИЯ И ПЕРЕСЧЕТ КРЫЛА С ОДНОГО УДЛИНЕНИЯ НА ДРУГОЕ

Установим связь между подъемной силой и индуктивным сопротивлением. Используем для этого формулы (2.20) и (2.21).

Рассмотрим наиболее выгодные крылья (с минимальным индуктивным сопротивлением). Для этих крыльев

&i=nKAi. (4.1)

Из формзлы (2.20) мол<но коэффициент А\ выразить через € :

И, подставив его в (4.1), получить связь между коэффициентом индуктивного сопротивления и коэффициентом подъемной силы:

г(0

(4.2)

В плоскости {Сх, Су) зависимость (4.2) изображается в виде параболы, называемой параболой индуктивного сопротивления (рис. 52).

Индуктивное сопротивление, как уже говорилось выше, связано со скосом потока, возникающим вследствие свободны.\ ви.х-

1)ей, сбегающих с задней кро.мки. Если скоса потока нет, то индуктивное со-протпвленне равно нулю. В реальной жидкости кроме силы индуктивного сопротивления на крыло действует еще сила так называемого профильного сопропшления, которое складывается из сопротивления трения и сопротивления давления. Коэффициентом полного сопротивления называется величина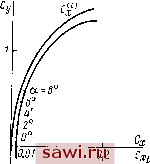

Рис. 52.

где /?полн сумма профильного и индуктивного сопротивлений.

В широком диапазоне условий коэффициенты Сх, Су можно считать постоянными при заданной форме тела и его положении по отношению к потоку. При различных углах атаки получается кривая Сх = Сх{Су), называемая полярой крыла (см. рис. 52).

При небольших углах атаки справедливо следующее соотношение:

Сх {Су) - Ci?* {Су) = Cf = const. (4.3)

Величина c!f* называется коэффициентом профильного сопротивления. Тот факт, что при небольших углах атаки коэффициент Cif постоянен, дает возможность получить простые формулы для пересчета крыла с одного удлинения на другое.

Пусть имеется поляра крыла для удлинения К ~ К[, надо построить поляру для крыла с удлинением X = Аг. Воспользуемся формулой (4.3):

CfC + CiX)

(4.-1)