Приравнивая коэффициенты, получаем

(9.5)

Формула (9.5)-формула преобразования компонент тензора второго ранга при переходе от одной системы координат к другой. Следовательно, таблица e,ft есть аффинный ортогональный тензор второго ранга - тензор скоростей деформаций.

С тензором скоростей деформаций связана квадратичная форма F, имеющая вид (8.10). Всегда можно ввести такие координаты li, о, з, в которых квадратичная форма примет вид

В этих координатах тензор скоростей деформаций будет

(9.6)

(9.7)

Оси, в которых тензор e/j. имеет вид (9.7), называются главными осями тензора скоростей деформаций (это главные оси квадратичной формы F). Величины еь ег, ез, которые входят а (9.7), называют главными скоростями деформаций. Известно, что еь 62, ез являются корнями кубического уравнения

11-Я 8i2

21 22 - Я,

ез1 ез2

е,з - Я

= 0.

(9.8)

Корни этого уравнения всегда вещественны. Вещественность корней уравнения (9.8) следует из симметричности матрицы e,fe. Запишем уравнение (9.8) в виде

-3--/i2-/2X + /3 = 0.

(9.9)

Поскольку главные скорости деформации е,- - инварианты, инвариантами должны быть и коэффициенты уравнения (9.9). Эти коэффиценты /ь /г, h называют соответственно линейным, квадратичным и кубичным инвариантами тензора скоростей деформаций. Наиболее простой вид имеет линейный инвариант/]. Это просто свертка тензора е,*:

dv\ j dv2 дУз дхг

/1 = 811 + 622 + Баз = +

dxi дхг

Коэффициенты /2, /3 можно записать в виде

= divv.

812 822

822 823 832 833

/3==dete .

833 813

831 811

§ fO. смысл КОМПОНЕНТ ТЕНЗОРА СКОРОСТЕЙ ДЕФОРМАЦИЙ

Выражения для компонент скорости деформации имеют вид (8.15). Скорость деформации Уд будет определена для любой точки (при известных , ц, t,) частицы, если задана таблица (8.17). Выясним физический смысл величин - компонент тензора скоростей деформаций (8.17). Рассмотрим частные случаи.

1. Пусть Ёхх ф О, все остальные ziu = 0. В этом случае тензор

е О О

(10.1)

Формулы (8.15) примут вид

f дх = бххЕ, Уд = дг == о

(10.2)

Таким образом, тензору (10.1) соответствует однородное растяжение (ехх > 0) или сжатие {zxx < 0) объема вдоль оси X (рис. 2). Из (10.2) следует, что

- скорость растяжения

8 V к -

(сжатия) элементарного объема вдоль оси X, приходящаяся на единицу длины. Аналогичный смысл имеют Zyy и Zzz- Итак, диагональные элементы тензора скоростей деформаций - относительные скорости равномерного растяжения элементарного объема вдоль координатных осей.

2. Пусть теперь Zxy = e Ф О, все остальные е;* = 0. Тогда

Рис. 2.

Соответственно

ах = .хуЦ, Vjy = Byxl, == 0.

(10.4)

Отсюда видно, что точки оси ti( = 0) испытывают сдвиг в направлении оси I, пропорциональный расстоянию ц, точки оси I -сдвиг в направлении оси ц (рис. 3). Таким образом, имеет место скашивание прямого угла (в данном случае между осями I и т]). Составляющие

ах Удг/

ху ух

имеют смысл скорости скашивания прямого угла. .Аналогичный смысл имеют другие боковые ко.мпоненты (8.! 7). В общем случае, когда тензор Т имеет вид (8.17), деформацию элементарного объема можно представить как суперпозицию деформаций растяжений (сжатий) относительно тре.х координатных осей и деформаций сдвига. Если тензор скоростей деформаций отнесен к своим главным осям , т), , то скорость деформации будет иметь проекции

vK = \\, vy = E.\, Удг = е.зС. (10.5)

Таким образом, самая общая деформация частицы может быть представлена как дефор.мация растяжения относительно тре.х главных осей деформации.

Из (10.5) следует, что если уд = О, то 81 = 62 = 83 = 0. Это значит, что отсутствие деформации соответствует нулевому тензору (в главных осях). Но если тензор нулевой в главных

осях, то он будет нулевым и во всех других осях, т. е. из од = О следует, что Bik - 0. Очевидно, что в этом случае и все инварианты тензора е равны нулю: 1\ =z I2 = I-i = 0.

§ 11. СМЫСЛ КОМПОНЕНТ ВИХРЯ СКОРОСТИ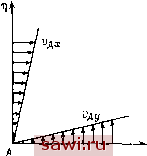

В § 8 мы установили, что скорость любой точки жидкой частицы может быть представлена в виде

Рис.3. Ув = Ул + 4-ОХр+Уд,

где Ул -скорость полюса; Уд -чисто деформационная скорость; 2

-QXP-скорость точки во вращательном движении затвердев-

шей жидкой частицы с угловой скоростью - й.

Вектор й = rot V = 2(0 - удвоенная угловая скорость, с которой затвердевшая жидкая частица вращается вокруг оси, проходящей через полюс. Проекции вихря скорости

dVu

дУц dvx дх ду

Проекцию вектора угловой скорости на какую-либо ось можно одновременно рассматривать как угловую скорость вращения