Остановимся на случае, когда обе стенки неподвижны. Тогда 0[ = У2 = О, и решение (3.4) примет вид

(3.6)

Выражение в скобках в силу < /г неотрицательно, так что жидкость всегда движется в направлении падения давления. Максимальное значение скорости Vx достигается при у = Q. Зависимость Vx = Vxiy) имеет вид параболы (рис. 53).

У77,

777777/,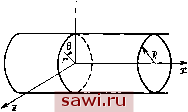

Рис. 53.

Рис. 54.

Подсчитаем расход жидкости через сечение между пластинами при толщине слоя вдоль оси z, равной единице:

(3.7)

т. е. расход прямо пропорционален падению давления, кубу расстояния между пластинками и обратно пропорционален коэффициенту вязкости.

§ 4. ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ В КРУГЛОЙ ТРУБЕ

Рассмотрим установившееся течение вязкой жидкости в круглой трубе радиуса R (рис. 54). Труба неподвижна, ось х. совпадает с осью трубы. Для определения поля скоростей надо решить уравнение (1-13) при условии, что в любом поперечном сечении на контуре трубы г/ -f 2 = i? скорость равна нулю. Естественно ввести цилиндрические координаты. Переходя от координат у, Z к координатам г, 9, получим г/ = г cos О, z - = г sin 9,

]сследусмос течение осесимметрично, поэтому Vx зависит лишь от г. Уравнение (1.13) при этом становится обыкновенным дифференциальным уравнением второго порядка.

Таким образом, задача свелась к решению уравнения

dVx , 1 dvx i /д , ч

dr г dr ц Ах -

при условии

t.Ufi = 0. (4.2) Уравнение (4,1) можно переписать в виде

Интегрируя, получим

dvx J ±,P Sl\r dr ц Дх 2

Постоянную Ci следует положить равной нулю, так как иначе на оси трубы г = О скорость будет неограниченной величиной, что не имеет физического смысла. Постоянную Сг находим из граничного условия (4.2):

Дх4 - д,Дх4 V/

Таким образом, для поля скоростей вязкой жидкости внутри трубы имеем формулу

-==-i4f(-)- (4-6)

Формула (4.6)-формула Пуазейля.

Подсчитаем расход жидкости через поперечное сечение трубы:

\ Vx

о Jo

(4-7)

Таким образом, расход пропорционален падению давления, четвертой степени радиуса трубы и обратно пропорционален коэффициенту вязкости. Обычно интересуются падением давления

в зависимости от Q, R, р. Формула (4.7) используется

также для экспериментального определения коэффициента вязкости.

Полученное решение (как и решение предыдущей задачи в § 3) не всегда хорошо согласуется с экспериментом. Оказывается, что качественная картина течения существенно зависит от безразмерного параметра Re, введенного Рейнольдсом. Числом

Рейнольдса называют величину Re=-; где v и / - харак-256

терные для данного течения скорость и размер. Для течений в трубах за характерную скорость принимают среднюю скорость

ц 9. LD2

VcpR

Если Re = 1000 -7- 1100, то имеется хорошее совпадение

теории с экспериментом. При Re (1000-ь1100) происходит резкое изменение картины течения. При небольших Re каждая частица жидкости движется по прямой, движение слоистое, спокойное. Такое течение называется ламинарным. При Re > 10 каждая из частиц жидкости совершает хаотическое движение, течение перестает быть одномерным и стационарным. На среднюю скорость накладываются дополнительные составляюшие, зависящие от времени и координат. Такое течение называется турбулентным.

Формулы (3.6), (4.6) справедливы только для ламинарных течений. Число Re, при котором происходит переход течения от ламинарного режима к турбулентному, называется критическим числом Рейнольдса. Цифра 10, которая приводилась выше, относится к обычным технически гладким трубам. Однако на самом деле переход ламинарного режима в турбулентный - явление сложное. В частности, число RCkp при специальных условиях может быть сильно увеличено. Рейнольдсом был проведен следующий опыт. Брались специальным образом подготовленные очень гладкие трубы с очень гладким входом. Жидкость подавалась в трубу из специальных баков, в которых она отстаивалась в течение 2-3 недель. Тогда критическое число Re возрастало до 10 Таким образом, переход к турбулентному режиму существенно зависит от уровня начальных возмущений. Кроме того, существует и нижняя граница Rep . Если Ре<Ре1Гр . то течение всегда ламинарное. Известно также, что задержке перехода к турбулентному режиму способствует добавление в жидкость молекул полимеров.

Примечание. Решение (4.4), полученное для осесимметричных течений в круглой трубе, содержит две произвольные постоянные. В этом решении равенство нулю постоянной Сг обеспечивало ограниченность скорости внутри трубы. Для случая осесимметричных установившихся течений жидкости внутри кольцевой трубы Ri < f/ + < /?2 решение (4.4) также справедливо, только постоянные С, и Сг должны быть определены из условий прилипания жидкости к каждой из стенок трубы Ri и R2. В самом общем случае эти условия имеют вид

1г = Л1

где Vi и V2 - скорости, с которыми трубы движутся параллельно своей оси (оси х). Если стенки труб неподвижны (ui = V2 = 0), то движение жидкости может иметь место только за счет