§ 3. ПАРАДОКС СТОКСА

Рассмотрим плоскую стационарную задачу. Систему уравнений (1.8) можно тогда записать в виде

(dvx , dvx\ dp \ дх ~df~)~~d7

fdvy , dvy\ dp dVx dVy

+ - = 0.

dx dy

Если использовать эти уравнения для получения решения задачи об обтекании кругового цилиндра, когда граничные условия имеют вид

Vx L = V, Vy L = 0, p L = p,

TO оказывается, что такая задача вообще решения не имеет, так как невозможно удовлетворить одновременно условиям на теле и на бесконечности. Единственное решение задачи, удовлетворяющее условиям прилипания на теле, есть тождественный нуль. Такое же утверждение верно для произвольного цилиндра. Это - парадокс Стокса, а именно: если рассматривается обтекание цилиндра произвольной формы потоком вязкой жидкости, то уравнения Стокса для стационарной задачи в плоском случае решения не имеют. Возникает вопрос: справедливы ли те предположения, которые были использованы при переходе от уравнений Навье - Стокса к уравнениям Стокса. Для ответа на этот вопрос проверим, справедливы ли эти предположения в задаче об обтекании шара при том конкретном виде поля скоростей, которое мы имеем в этом случае. Если по формулам (2.4) вычислить члены, входящие в уравнения Навье - Стокса, и

сравнить выброшенные члены Vi -~- и оставленные grad р, pAv,

го окажется, что в некоторой окрестности сферы отброшенные члены действительно малы по сравнению с оставленными. Однако на больших расстояниях от сферы отброшенные члены много больше сохраненных. Следовательно, предположения Стокса заведомо неверны на больших расстояниях от тела, в связи с этим возникают следующие вопросы: не в этом ли состоит причина парадокса Стокса, нельзя ли усовершенствовать уравнения Стокса, сохранив линейность, но обеспечив корректность на больших расстояниях от тела.

Причина несуществования стационарного решения (парадокс Стокса) может быть в какой-то мере выяснена, если рассматри-

шается с угловон скоростью (оь а внешний - со скоростью (Оо-Для решения задачи удобно ввести цилиндрические координаты г, Q, X и записать в этих координатах систему уравнегтн вязкой

жидкости. Для этого надо найти выражения divv,-, grad/л,

Ду в этой системе координат. Естественно предполагать, что скорость направлена по касательной к окружности г - const и зависит так же, как и давление, только от г, т. е. Vx - Vr = О, vo = v{r), p = p{r). Полученная система уравнений применительно к рассматриваемой задаче, когда двилсение установившееся, принимает простой вид и позволяет сразу получпть решение задачи в виде

Постоянные С\ и Сг определяются из граничных условий. Однако для решения рассматриваемой задачи мы используем другой путь.

Чтобы найти зависимости v = v{r), запишем закон сохранения момента количества движения в слое R\ у-\-z- г, г < R2 (рис. 55). Пусть М - момент сил, действующих на этот слой. Поскольку течение плоское, вектор М направлен по оси х. В силу стационарности движения имеем равенство Л1 == 0. Очевидно, что М = Ml + Mr, где Ml - момент сил, действующих на внутренний цилиндр, М - момент сил вязкого трения, приложенных к цилиндру радиуса г. Величина этого вектора

= 5 / (т,ег е) = г2 5 т,е dQ. р 55

Здесь Тге - проекция на ось 9 (т. е. на направление v) напря-л<ения, действующего на площадку с нормалью г. При наших предположениях оно зависит только от г, поэтому

Mr = Хге2лг-.

Таким образом, закон сохранения момента дает равенство

т,е2.ттг2 + Ml = 0. (6.1)

Пусть угол 9 отсчитывается от оси у. Очевидно, что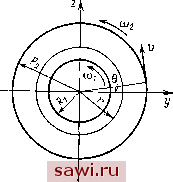

dVy ~dz

Поскольку T-e не зависит от 9, последнее соотношение верно при всех 9. Таким образом.

Далее имеем Vy = - v sinB = - v у, = и cos 9 = и у- и

=0 dz \ Г J г=0 г , ,

v , ( d v\ - - Л. (А-ИЛ

z-a г \dr г ) г 2=0 \dr г )

Используя ЭТИ равенства, на основании (6.2) получим

T.e = Mrf(f). (6.4)

Подставляя (6.4) в (6.1), получим уравнение для отыскания v: M, + 2nr3(x-(f) = 0. (6.5)

Общее решение этого уравнения дается формулой

о = С,г + . (6.6)

где <2 = - Постоянные С\ и Сг определяются из граничных условий

ИЛИ, более подробно,

ад + - = Мь С,/?г + = 2 2. (6.8)

Решая систему (6.8), получим

),;?2- )2/? /?/2( 2- l) ggj

о2 г,2 п2 п2

J<1 - <2 М - 2

Таким образом, распределение скоростей между соосными цилиндрами дается формулой

(0l.R-fi)2/?2 . , /??/?(fi>2- l) 1

J\j ~~ A2 Aj A2

Имея формулу (6.10), легко вычислить те и Mr:

T.e = l-ir(f) = -2(i-. М, = т,е2яг2 = -4яцС2. (6.11)

где Сг имеет вид (6.9).

Заметим также, что, измеряя в эксперименте Mr, можно определить вязкость.