где числа Re и Fr вычисляются по скоростям на бесконечности. Обычно условия 1) и 2) подразумеваются выполненными, и тогда условия подобия записываются в виде

Re(i) = Re<2), Fr() = Fr(2). (3.13)

Заметим, что число Re содержит коэффициент v. Этот параметр подобия характерен для вязкой жидкости. В идеальной жидкости V = О и Re - оо. Подобие же по числу Фруда имеет смысл как для вязкой, так и для идеальной жидкости.

Рассмотрим теперь следующий вопрос. Пусть произведен опыт с моделью в аэродинамической трубе. Когда можно использовать данные этого эксперимента для реальных обтеканий? Предположим, что условия 1), 2) выполнены и g - поле силы тяжести. Пусть индексом 1 отмечаются величины, связанные с экспериментом в трубе. Тогда для подобия течений нужно выполнение равенств

1 Ло i!VLlVL (3 14)

Если оба эксперимента проводятся в условиях Земли, то g\ = = g2 = g, если среда одна и та же (например, воздух), то, кроме того, VI = V2. Тогда условия (3.14) перепишутся следующим образом:

(o< V (o*2)V 1 оо 2 оо> а, аг

Обычно размер модели ai меньше размеров реального тела. Поэтому для выполнения первого условия необходимо, чтобы выполнялось неравенство v- > а для выполнения второго условия необходимо выполнение неравенства < v. Таким образом, подобие по числам Re и Fr приводит к противоречивым условиям.

Один из возможных выходов из этой трудности связан с проведением экспериментов при высоких давлениях. Тогда за

счет изменения плотности (-jj = Vj < Va в принципе можно добиться подобия по Re при uj,* < d<>. Однако дело в том, что числа Re и Fr не во всех условиях одинаково существенны. При исследовании волновых процессов (в частности, качки корабля), когда существенно влияние силы тяжести, моделируют по числу Фруда. При исследовании силы сопротивления, наоборот, существенно влияние вязкости - моделируют по числу Рейнольдса.

Можно в уравнения (2.1) ввести вместо функции функцию л:

л = - {gxX + gyy + gzZ) + J. 9* 267

перепада давлений ф . Безнапорное движение жидкости (- = 0 возможно если хотя бы одна из стенок переме-

щается.

§ 5 ТЕЧЕНИЕ В ТРУБЕ ЭЛЛИПТИЧЕСКОГО СЕЧЕНИЯ

Рассмотрим установившееся течение в бесконечно длинной неподвижной трубе с осью, направленной по оси х, сечением

+-р- 1. Скорость Vx должна удовлетворять уравнению

+ = А4£ (5,1)

ду dz р, Ах

и граничному условию на контуре

t;.lii,=0. (5.2)

а? Ъ--

Будем искать v в виде

и, = л(1---). (5.3)

При постоянном А функция (5.3) удовлетворяет условию прилипания (5.2). Следовательно, достаточно подобрать постоянную А так, чтобы выполнялось равенство (5.1). Вычисляя производные функции (5.3) и подставляя их значения в уравнение (5.1), получим

\а Ъ ) - р. Ах ~ 2ц а-\-Ь Ах Следовательно,

2ii Ах а+ Ь ~ Ч~ 1) (4)

1 Ар аЬ

Vx =------

При а = Ь = г из (5.4) получим формулу (4.6) для круглой трубы. Соотношение (5.4) подтверждается экспериментом для ламинарных течений.

Замечание. Пусть имеется неподвижная цилиндрическая труба с контуром I в поперечном сечении. Задача о течении

жидкости в такой тр (1.13) с условием v

убе сводится к интегрированию уравнения = 0. Такую задачу можно вообще ре-

шать для сечения любого вида.

§ 6. ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ МЕЖДУ ДВУМЯ ВРАЩАЮЩИМИСЯ СООСНЫМИ ЦИЛИНДРАМИ

Рассмотрим стационарное течение жидкости между двумя бесконечно длинными соосными круговыми цилиндрами радиусов R\ и Ri при отсутствии массовых сил. Направим ось х вдоль оси цилиндров, Предположим, что внутренний цилиндр вра-

шается с угловой скоростью соь а внешний - со скоростью Ыз. Для решения задачи удобно ввести цилиндрические координаты r,Q,x и записать в этих координатах систему уравнений вязкой

жидкости. Для этого надо найти выражения divv,-, grad

Ду в этой системе координат. Естественно предполагать, что скорость направлена по касательной к окружности г = const и зависит так же, как и давление, только от г, т. е. Vx = Vr = О, ve = v{r), p = p{r). Полученная система уравнений применительно к рассматриваемой задаче, когда движение установившееся, принимает простой вид и позволяет сразу получить решение задачи в виде

Ve = Cir +

Постоянные Ci и С2 определяются из граничных условий. Однако для решения рассматриваемой задачи мы используем другой путь.

Чтобы найти зависимости и = и{г), запишем закон сохранения момента количества движения в слое Ri г, г < R2 (рис. 55). Пусть М - момент сил, действующих на этот слой. Поскольку течение плоское, вектор М направлен по оси х. В силу стационарности движения имеем равенство М = 0. Очевидно, что М = Ml + Mr, где Ml - момент сил, действующих на внутренний цилиндр, М - момент сил вязкого трения, приложенных к цилиндру радиуса г. Величина этого вектора

2л 2л

Мг = \г (т,ег dQ) = г2 5 т,9 dQ. 55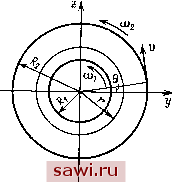

Здесь Ггв - проекция на ось 6 (т. е. на направление v) напряжения, действующего на площадку с нормалью г. При наших предположениях оно зависит только от г, поэтому

Mr - Хго2лг.

Таким образом, закон сохранения момента дает равенство

т,е2лг2 + Ml = 0. (6.1)

Пусть угол 9 отсчитывается от оси у. Очевидно, что

Т/-е 19=0 - Т,г 1г=0