КИМ выражениям для интегралов от этих функций по объему элемента. (Явные формулировки для квадратичных элементов можно найти в [10.4] и [10.51, а для элементов с кубическим полем перемещений в [10.6].) Элементам Т48 уделяется внимание из-за их эффективности при решении прикладных задач и из-за того, что на их примере демонстрируются операции, которые нужно выполнить, если перемещения записываются в терминах обобщенных координат, а не в виде функций формы.

10j.2. Элемент с линейным полем перемещений [10.19]

Линейные поля перемещений (и, v, w) можно записать в тетраэдральных координатах L J = Li Lj La Li J (см. разд. 8.6) в виде

u=LLJ{u}, t;=LLJ{v}, w=iL \{v,}, (10.11)

u=L i а з ij, (10.12)

и аналогично для {v} и {w}. Замечая, что, согласно (8.29),

Li==

g-[(VOL),.-f Ci.x + C2.y + C3.z],

где (vol), с,., Cj. и Сз выражаются в разд. 8.6 в терминах узловых координат Xi, . . ., 24. Применяя соотношения (10.2) между деформациями и перемещениями к уравнениям (10.11), приходим к следующей форме уравнения (10.6):

{v} = [D]{A}, (10.13) {w}

где Lcf J = Lci.cici,cj J , и аналогичные представления справедливы для \ С2 \ и LsJ; матрица 0J, имеющая размерность 1X4,- нулевая матрица-строка. Линейное поле перемещений обусловливает постоянство деформаций внутри элемента. Поэтому такой элемент часто называют тетраэдральным элементом с постоянной деформацией (CSTh-элемент). Если [Е] определено в соответствии с (10.3) и все элементы матрицы [D] постоянны, то из (10.8) получим выражение для матрицы жесткости тетраэдрального элемента в внде [k] = [D] [Е] [D](vol), где объем элемента (vol) подсчитывается, как указано в разд. 8.6.

На практике чрезвычайно трудно задать конфигурацию конечно-элементной модели только одним указанным элементом. Проб-

лема заключается в правильном объемном расположении тетраэдров без пустот и т. д. Поэтому вычислительные программы часто предусматривают непосредственное задание шестигранных элементов, которые автоматически составляются из фиксированного числа тетраэдров. На рис. 10.4 изображен один из таких суперэлементов , включающий пять тетраэдров.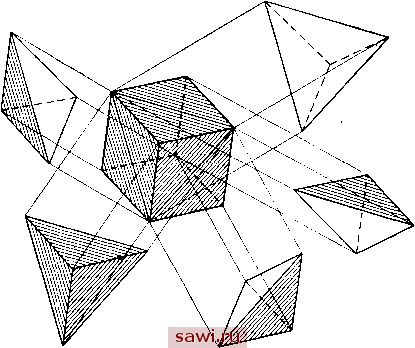

Рис. 10.4. Шестигранник, составленный из пяти тетраэдров. 10.2.3. Элементы высших порядков [10.6J

Простой способ построения элемента Т48 основан на разложении величин в ряд по тетраэдральным координатам в виде

-f LLa, + LaL.a, + LLa, + (LIL - ЦЦ) a -f + {LlL,-mi)щ, + {L\L,-L,Ll)-f

+ (LlL,-L3Ll)ai,+{L\L,-L,Ll)a + mLi-L,L\)ai,. (10.14)

Поля перемещений v м w определяются аналогичным образом, поэтому полный набор обобщенных параметров перемещения может быть представлен как {а}= ai...a8 J.

Теперь порядок построения матрицы жесткости соответствует изложенному в предыдущих главах. Выписанные поля перемещений дифференцируют согласно соотношениям между деформациями и перемещениями (10.2) и приходят к уравнениям вида е=[С] {а}. Кроме того, в каждой из четырех вершин определяются функции перемещений и их первые производные. В результате получают 48 уравнений, записанных в виде {Л}=[В] {а}, где {А} содержит степени свободы, представленные в (10.10) для поля и и в аналогичных формулах для полей v н w. Следовательно, матрица жесткости дается формулой (10.8а):

[к] = ([В]-У Г 5 [Cf [Е] [С] d (vol)l [В]-.

-vol

Очевидно, полученное выражение слишком сложно для задания явного представления.

Изложенная подробно в [10.6] процедура построения матрицы жесткости для рассматриваемого элемента существенно отличается от приведенной выше. В указанной работе приводятся в виде таблиц матрицы жесткости в обобщенных координатах и матрицы преобразования обобщенных координат в узловые. Знание явных выражений для основной матрицы жесткости, как показано в разд. 8.2, где строится матрица жесткости, соответствующая обобщенным смещениям {а}, позволяет построить целое семейство матриц жесткости тетраэдральных элементов для полей перемеще1шй в виде полных кубических полиномов обобщенных параметров.

Развивались и другие подходы к построению матрицы жесткости элемента Т48. Так, в [10.1] вначале строится полный (двадца-тиэлементный) кубический полином в объемных координатах, а далее в предположении, что перемещения меняются по квадратичному закону вдоль граней элемента, число членов доводится до 16. Для определения элементов в криволинейных координатах используются также различные метрики. В [10.2] полный квадратичный полином в объемных координатах (10 членов) дополнен шестью членами, взятыми из кубического разложения.

10.3. Прямоугольные шестигранные элементы 10.3.1. Общие замечания

На рис. 10.5 изображено базисное семейство прямоугольных шестигранных элементов, степени свободы которых представляют собой лишь трансляционные перемещения. Это семейство называется лагранжевым, так как поля перемещений, на основе которых они строятся, задаются с помощью лагранжевой интерполяции, описанной в п. 8.3.1. Простейший элемент из этого семейства изображен на рис. 10.5 (а) и строится на основе линейных полей перемещений.