ПОЛНОСТЬЮ определяемых степенями свободы в восьми вершинах. Обобщение на квадратичные и кубичные поля перемещений приводит, как показано соответственно на рис. 10.5(b) и (с), к появлению внутренних узлов. Указанные внутренние узлы можно исключить из рассмотрения с помощью стандартной процедуры конденса-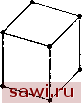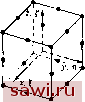

(а) (Ь) (с)

Рис. 10.5. Лагранжево семейство шестигранных элементов (внутренние узлы не изображены): (а) линейный: 8 узлов, 24 степени свободы; (Ь) квадратичный: 27 узлов, 81 степень свободы; (с) кубический: 64 узла, 192 степени свободы.

ции (см. разд. 2.8). Кроме того, с помощью описанного в разд. 8.7 приема, преобразуя лагранжевы интерполяционные функции, можно построить функции формы, которые записываются только в терминах внешних узлов.

Используя интерполяцию Эрмита (п. 8.3.2), можно также построить прямоугольный шестигранный элемент со степенями свободы в виде значений производных в вершинах элемента. Для построения базисного элемента из этого семейства необходимо задание кубических полей перемещений, причем общее число степеней свободы для элемента достигает 192.

Хотя построение прямоугольных шестигранных элементов все более высокого порядка с любым типом степеней свободы теоретически возможно, все же на практике ограничиваются лишь несколькими основными видами. Характеристики этих элементов сведены в табл. 10.2 [10.3]. Из представленных в таблице элементов обсудим подробно задание полей перемещений лишь для случаев а, b и с, taK как именно эти элементы используются в рассматриваемых ниже тестовых численных экспериментах и широко применяются на практике. Описание полей перемещений для случаев d w е можно найти соответственно в [10.7] и [10.8].

10.3.2. Прямоугольный шестигранник с линейным полем перемещений

В дальнейших построениях удобно поместить начало координат в центре элемента и выразить все координаты в безразмерном виде, причем указанные координаты , т] и задаются согласно методике разд. 8.7 (см. рис. 10.5(b)). Аналогично случаю плоских элементов, описанному в разд. 8.4, для полей перемещений при интерполяции

Таблица 10.2. Прямоугольные шестигранные конечные элементы

Обозначение Представление

Число узлов

Число степеней свободы, приходящихся

Замечания

на эле-нэ узел мент

8 3 24 Поля перемещений в виде линейных полиномов; и, v, W в качестве степеней свободы в каждом узле; подробнее см. [10.4, 10.9]

20 3 60 Поля перемещений в внде квадратичных полиномов; и, V, W в качестве степеней свободы в каждом уз-ле;см.[10.4, 10.10, 10.17]

32 3 96 Поля перемещений в виде неполных кубических полиномов; и, V, W в качестве степеней свободы в каждом узле; см. [10.4] и [10.14]

64 3 192 Поля перемещений в виде полных кубических полиномов с внутренними узлами; и, V, W в качестве степеней свободы в каждом узле; в изопараметрическом случае называется элемент LUMINA; подробнее см. [10.7]

8 12 96 Поля перемещений в виде неполного полинома пятой степени [10.13] либо эрмитовой полиномиальной интерполяции [10.8]; перемещения и производные от перемещений в качестве степеней свободы; изопараметрическое представление обсуждается в цитированной литературе

Лагранжа имеем

=LNJ{u}, c;=LNJ{v}, =LNJ{w[. (10.15)

причем

W = [D]

{V} {w}

(10.6а)

Если [Е] выбрана в соответствии с (10.3), то приходим к матрице жесткости, задаваемой выражением (10.8), т. е.

-vol

Явный вид этой матрицы приводится в 110.9J.

10.3.3. Прямоугольные шестигранники высших порядков

Как указывалось, можно легко построить шестигранный элемент более высокого порядка, применяя для этого интерполяцию Лагранжа требуемого порядка. Возникающие в этом подходе трудности обусловлены наличием узлов внутри элемента и на его гранях. Поэтому предпочтительнее использовать элементы, имеющие узлы только на ребрах, как, например, двадцатиузловой элемент, представленный в графе b табл. 10.2. В этом случае матрицы соотношений (10.15) имеют вид

NJ = LA/,...A/, J, {u}=L i... , J

и аналогичные выражения для {v) и {w}. Как отмечалось в разд. 8.7, этот вид функций формы с исключенными внутренними узлами не единствен. Широко используется и следующий альтернативный вид. В вершинах (с началом координат в центре)

A/,=V,(l + iy (l+mt) (1+Й,) ah+r\r\t+-2), (10.17)

а для типичного узла, находящегося в средней точке ребра,

, = 0, Л/ = ±1. С = ±1. ig,

A/, = V.(l-)(l+nn/)(l-f сед

Формулы, задающие связь этой функции с коэффициентами полиномиального разложения, а также альтернативные виды функций формы для 20 узловых элементов приводятся в IIO.IOJ.

Л/, = /,(1+11,)(1+ЛЛ/)(Ч-СС/). (10.16)

Построение матрицы жесткости для этого элемента осуществляется обычным способом. Поля перемещений (10.15) дифференцируются согласно соотношениям между перемещениями и деформациями (10.2). Приходим к формулам преобразования узловых смещений в деформации