Более сложное представление с 32 узлами дается в табл. 10.2 в графе с. Здесь функции формы в вершинах имеют вид (с началом координат в центре)

NiЧ,Л + Ш{\+mi){\+Ш)[9{l--ц+t,j~Щ\, (10.19)

а для типичных узлов, лежащих на ребрах в точках 1=±/з. ili = = ±1, Ci = ±l, имеем

NiU,(\-l-) (1 + 9?!,) (1+лл.) (l+Sti). (10.20)

Процедура преобразования выписанных полей перемещений в матрицы жесткости элементов совпадает с процедурой для шестигранника с линейным полем перемещений.

10.4. Сравнение численных результатов

В [10.1, 10.3, 10.4, 10.9] были проведены исследования относительной точности и эффективности некоторых тетраэдральных и шестигранных элементов, описанные в п. 10.3.1 и 10.3.2. На рис. 10.6 изображена задача, рассматриваемая в [10.4] в качестве тестовой

Точки, сво((одно перемещ,аюш,иеся в n/tocHocmu y-z

-- Момент =

800 1рунгп-дюйм

гпо г (дюйН)

7 по 3 {дюйм)-

Рис. 10.6. Консольная балка, используемая для изучения точности решений (из 110.4]) (размеры даны в дюймах).

ДЛЯ сравнения точности получаемых решений. Конструкция представляет собой консольную балку, к которой на конце приложен момент. Балка разбивается на 42 прямоугольных шестигранных элемента. Часть решений получена с помощью шестигранных элементов, образованных в результате объединения тетраэдральных элементов, например, как показано на рис. 10.4. Изучаемые элементы включают тетраэдры, построенные на линейных и квадратичных полях перемещений, что соответствует графам а и й в табл. 10.1, а также прямоугольным шестигранным элементам, построенным на линейных полях перемещений (10.16) - (10.18) (графа Ъ в табл.

10.2). Тетраэдральный элемент с квадратичным полем перемещений и двадцатиузловой шестигранный элемент приводят к тем же результатам при вычислении смещения конца балки, что и балочная теория. Тетраэдральный элемент (образованный, как показано на рис. 10.4, объединением пяти элементов) с линейным полем перемещений и шестигранный элемент с линейным полем перемещений приводят к результатам, соответственно на 39 и 10% меньшим, чем решение на основе балочной теории.

Нагрузка \

Гл злементоИ г по 10 дюймой

т элементов ~по 100 дюймов

Нагрузка I

п эпементой по 10 дюймов

т элементов по 10 дюймов

Рис. 10.7. Тестовые конструкции для изучения вычислительной эффективности метода (из [10.4]): (а) гибкая консоль; (Ь) жесткая консоль. Замечание. Обе конструкции имеют единичную толщину.

Для двух тестовых задач, изображенных на рис. 10.7, 10.8, приводятся результаты сравнения эффективности численного решения, измеряемой затрачиваемым машинным временем, для шестигранного элемента с линейным полем перемещений и двадцатиуз-лового шестигранника (графа b в табл. 10.2). Результаты показывают, что для тонкой балки (рис. 10.7(a) и 10.8(a)) двадцатиузловой элемент, очевидно, лучше. Этот элемент может воспроизвести линейный характер изменения деформаций по толщине балки, что характерно для изгиба. Сказанное выполняется и для короткой балки (рис. 10.7(b) и 10.8(Ь ), где наблюдается напряженное состояние более общего вида. В 10.4] приводится много других результатов, выходящих за круг вопросов, рассматриваемых в данной книге.

Приведенные в [10.4] результаты численных экспериментов подтверждают преимущество непосредственного построения шести-

(3,1)

h (30,2); ;:*-

[{(10,3)

- \00,2) (10,1)

(40,3)

10 20 30 40 50 Время счете, о

vet 5,3)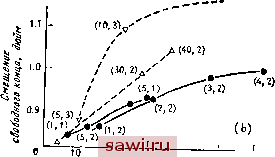

20 30 40

Вреня счета, с

Рис. 10.8. Результаты исследования вычислительной эффективности при расчете консольных балок (из [10.4]). (а) гибкая консоль (см рис. 10.7(a); (Ь) жесткая консоль (см. рис. 10.7(b). Обозначения-20-узловой шестигранник,---

шестигранник с линейным полем перемещений; (т, п) - размерность сетки.

гранного элемента по сравнению с составленными из тетраэдральных элементов согласно рис. 10.4. Для подтверждения этого высказывания требуется еще большее количество численных экспериментов. Различия в деталях при формулировке элементов, искусство программирования и вид электронно-вычислительных устройств влияют на получаемые разными исследователями выводы. Поэтому при анализе трехмерных конструкций проектировщики отдают предпочтение тетраэдральным элементам. Интересную сводку результатов практического применения указанных элементов можно найти в [10.11].