10.5. Изопараметрическое представпение

10.5. Изопараметрическое представление и анализ оболочек с помощью трехмерных элементов

Успех применения трехмерных элементов существенно зависит от имеющихся возможностей проведения высокоэффективного общего анализа системы, причем использование наиболее эффективных алгоритмов при построении алгебраических уравнений и их численном решении является обязательным [10.12].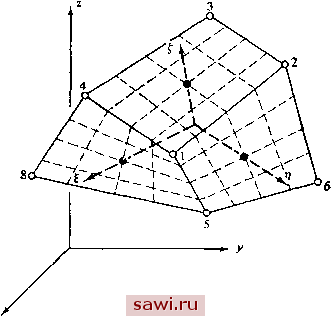

Рис. 10.9. Шестигранный элемент с линейным полем перемещений - изопараметрические координаты.

Другим фактором достижения максимальной эффективности анализа является использование изопараметрического представления геометрии трехмерных элементов. Если элементы ограничены плоскими, а не криволинейными гранями, то часть степеней свободы при общем анализе должна определяться соответственно геометрическим представлением. Число указанных степеней свободы существенно уменьшается, если использовать концепцию изопара-метрических элементов при задании криволинейных границ элемента. Тогда степени свободы максимально используются при определении поведения конструкции.

На рис. 10.9 иллюстрируется способ задания координатных осей

ДЛЯ изопараметрического представления шестигранника с линейным распределением перемещений. Поле перемещений для прямоугольной формы этого элемента, задаваемого формулой (10.16), записывается непосредственно через безразмерные координаты (S, Ц, С), изображенные на рис. 10.9. Таким образом, выполняя операции, описанные в разд. 8.8, можно непосредственно построить изопараметрическую форму этого элемента. Однако алгебраические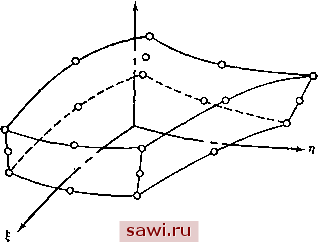

Рис. 10.10. Шестигранный элемент, используемый в качестве искривленного обо-лочечного элемента.

сложности таковы, что явное выражение для результирующих коэффициентов жесткости получить затруднительно даже для этого элемента, являющегося самым простым из шестигранников. В общем случае является существенным численное определение соответствующих энергетических интегралов. Читателю рекомендуется обратиться к работам [10.13-10.15] для ознакомления со многими аспектами формулировок нзопараметрических трехмерных элементов.

Изопараметрические трехмерные элементы полезны также для представления оболочечных конструкций. На рис. 10.10 изображен двадцати узловой изопараметрический элемент, построенный в виде, удобном для анализа подобных задач. Применение этих элементов при анализе толстых оболочек дает прекрасные результаты, однако прн уменьшении толщины элемента получаемое решение не стремится к решению для тонких оболочек. Как указывалось в п. 9.3.2, это происходит потому, что возникают члены, характеризующие избыточную жесткость в представлении энергии дефор.мации сдвига. В работах [10.16] и [10.17] показано, что можно получить хорошие

Литература 323

результаты для тонких оболочек, если аппроксимировать вкладе* энергии деформаций сдвига и сохранить точность задания слагаемых энергии нормальных деформаций. Хак как этот тип элемента требует выполнения численного интегрирования при подсчете энергии деформации, легко осуществить это, понижая порядок численного интегрирования выражений для энергии сдвиговых деформаций. Численные результаты обсуждаются в разд. 12.6.

Альтернативным подходом к анализу оболочечных конструкций с использованием трехмерных элементов является подход, при котором рассматриваются дополнительные несовместимые моды. Этот подход описан в п. 9.3.2 и обсуждается в [10.18]. Такая схема позволяет использовать простейший вид шестигранного элемента, который базируется на линейных полях перемещений и имеет только восемь узлов в вершинах шестигранника.

Литература

10.1. Hughes J. R., Allik Н. Finite Elements for Compressible and Incompressible Continua.-Proc. of Symp. on Application of Finite Element Methods in Civil Eng., Vanderbilt Univ., Nashville, Tenn., Nov. 1969. p. 27-62.

10.2. Rashid Y. R., Smith P. D., Prince N. On Further Application of the Finite Element Method to Three-Dimensional Elastic Analysis.-Proc. of Symp. on High Speed Computing of Elastic Structures, Univ. of Liege, Belgium, 1970, 2, p. 433-454.

10.3. Fjeld S. A. Three-Dimensional Theory of Elasticity.-In: Finite Element Methods in Stress Analysis.- Trondheim, Norway: TAPIR Press, 1969, p. 333-364.

10.4. Clough R. W. Comparison of Three Dimensional Finite Elements.-Proc. of Symp. on Application of Finite Element Methods in Civil Eng., Vanderbilt Univ., Nashville, Tenn., Nov. 1969, p. 1-26 (printed by the American Society of Civil Engineers).

10.5. Argyris J. H. Matrix Analysis of Three Dimensional Media-Small and Large Displacements.-AIAA J., 1965, 3. No. 1, p. 45-51. [Имеется перевод: Ракетная техн. и космон.- М.: Мир, 1965, № 1.]

10.6. Argyris J. Н., Fried I., Scharpf D. W. The TET 20 and the TEA 8 Elements for the Matrix Displacement Method.-Aero J., July 1968, 72, No. 691, p. 618-623.

10.7. Argyris J. H. The LUMINA Element for the Matrix Displacement Method.- Aero J., June 1968, 72, No. 690, p. 514-517.

10.8. Argyris J. H., Fried I., Scharpf D. W. The Hermes 8 Element for the Matrix Displacement Method.-Aero. J , July 1968, 72, No. 691, p. 613-617.

10.9. Melosh R. J. Structural Analysis of Solids.-Proc. ASCE, J. Struct. Div., Aug. 1963, 89, No. ST-4, p. 205-223.

10.10. Rigby G. L., McNeice G. M. A Strain Energy Basis for Studies of Element Stilfness Matrices.-AIAA J., 1972, 10, No. 11, p. 1490-1493. [Имеется перевод: Ракетная техн. и космон,-М.: Мир, 1972, № П.]

10.11. Anonymous. Three-Dimensional Continuum Computer Programs for Structural Analysis.-ASME Special Publication, 1972.

10.12. Rashid Y. Three-Dimensional Analysis of Elastic Solids.-Int. J. Solids and Struct., Part I, 1969, 5, p. 1311-1332; Part II, 1970, 6, p. 195-207.

10.13. Zienkiewicz O., Irons В., Scott F. C, Campbell J. S. Three-Dimensional