симметрии

г=0.5-

г=?.0-

о Решение методом конечны;< э/1ементо}

- Точное решение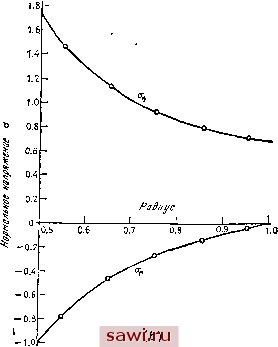

Рис. 11.5. Анализ толстостенного цилиндра, находящегося под действием внутреннего давления, (а) Конечно-элементное представление; (Ь) вычисленные напряжения.

угольному элементу, затруднительно. Тем не менее выписанные выше соотношения приводились в различном виде, например, в [11.2-11.4]. Формулы и сведенные в таблицы коэффициенты для основных членов элементов высших порядков представлены в [11.5] и [11.6]. Простые приближенные формулировки для осесимметрич-ного треугольника основаны на использовании среднего радиуса (например, значения в центре элемента), рассматриваемого в качестве константы интегрирования. Точность этой аппроксимации зависит от близости элемента к оси вращения.

При сравнении с классическими решениями установлено, что треугольный кольцевой элемент обеспечивает высокую точность, и это свойство, по-видимому, сохраняется и при решении прикладных задач. На рис. 11.5 изображено конечно-элементное представление для задачи расчета толстостенной трубы, находящейся под

. 30 о

i 20 10 -

По теории тонкил оЛ/ючек

4 8 17 16 20 24 28 32 Нис/!о рз/toS Sdo/it срединной поверхности

Рис. 11.6. Анализ сегмента сферы с использованием треугольных кольцевых элементов [11.3]. С любезного разрешения журнала AIAA Journal; w - перемещение в точке Со (в дюймах); нагрузка в центре равна 965 фунтов.

действием внутреннего давления. Используется довольно грубая сетка элементов. Различие между точным и численным решениями практически отсутствует.

Во второй задаче (рис. 11.6) анализируется сегмент жестко закрепленной сферической оболочки при действии сосредоточенной силы в ее вершине [11.31. Для сравнения приводится решение этой задачи с применением тонких оболочечных конечных элементов. Очевидно, что осесимметричный сплошной конечный элемент обеспечивает сходимость к решению, несколько отличающемуся от решения, полученного на базе тонких оболочечных конечных элементов. Различие объясняется расхождением между моделью поведения толстых оболочек и упрощенным представлением, даваемым теорией тонких оболочек.

11.3. Произвольные нагрузки

Нагрузки, действующие на осесимметричную конструкцию, не обязательно должны быть распределены осесимметричным образом. Примером реальных нагрузок указанного типа могут служить ветровые нагрузки на трубы или другие цилиндрические конструкции. Кроме того, при землетрясениях силы инерции, возникающие в результате ускорения поверхности земли, обусловливают неосесим-метричнъте нагрузки на резервуары и толстостенные цилиндрические конструкции. В том случае, когда распределенная нагрузка Т меняется лишь вдоль окружной координаты 9 и представляется небольшим числом членов разложения в ряд, можно сохранить большую часть преимуществ, изложенных в предыдущем разделе формулировок. Ниже опишем способ обобщения последних с целью учета неосесимметричных нагрузок.

Во-первых, предполагается, что усилия Т разбиваются соответственно на радиальные, окружные и осевые компоненты Т, Tq и Tj. Тогда, применяя стандартную процедуру разложения в ряд Фурье (см. 1П.7]), построим следующие аппроксимации:

7 , = S Tl cosпв + Tfrslnпв,

Гй = -En sinrtG -f Erg cosrte, (11.23)

f , = S Tl cos ne + Y.Tl sin fiG,

где каждый член в каждом из разложений называется гармоникой, а п - порядком гармоники. Суммирование производится по я, причем в сумме столько членов, сколько необходимо для описания изменения нагрузок в окружном направлении. Верхними индексами S отмечены симметричные компоненты нагрузки, а индексом а - антисимметричные компоненты. Представительные компоненты радиальной нагрузки изображены на рис. 11.7. Результирующие перемещения имеют соответствующий вид

и = S а cosл9 + S п sin яО,

у=-5]c; sinn0-f Sfncosne, (11.24)

11)=. К cos fiQ + sin nO,

где и , V и пу- симметричные компоненты смещения, а н , V и и,а антисимметричные компоненты. Эти компоненты задаются в терминах степеней свободы с помощью привычного представления через функции формы

LN J {u[, LN J

i = LN,J{v}, t=LN Jv-}, (11.25)