где {и?,}, . . ., {w°} - векторы, имеющие компонентами соответственно степени свободы элемента для симметричных и антисимметричных членов п-й гармоники, a N J, \ NJ и La/J - векторы, включающие функции формы для компонент перемещений , v и W. Они являются функциями только координат г и г.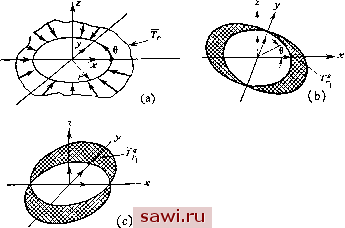

Рис. 11.7. Несимметричное радиальное иагружение и первые гармоники, (а) Распределение несимметричного радиального нагружения; (Ь) первая осесимметрич-ная гармоника; (с) первая антисимметричная гармоника.

Ввиду того что теперь необходимо учитывать изменения величин и в окружном направлении, уравнения, связывающие перемещения и деформации, примут вид

ди , Гл. = 57 +

ди Or

dw IF

дш I

(11.26)

dv I dw I ди , dv v

V9 = 5i + 7ae У=Тдд + д?-Т-

Объединим эти компоненты деформации для п-й гармоники в следующий вектор-столбец:

Отвечающая этому вектору (бхб)-матрица жесткости материала задается выражением (10.3).

Если в соотношения между деформациями и перемещениями (11.26) подставить выражение для перемещений п-й гармоники (11.24), получим систему уравнений, связывающую деформации и узловые перемещения. Используя обычные обозначения для преоб-

разованпй этого типа, запишем

= [D%]{\%}+[D]{K}, (11.27)

[D5,] и [D°] представляют соответственно симметричные и антисимметричные преобразования перемещений в деформации и

LA j = LLu,!JLv,1JLw. j J.

Теперь можно определить потенциальную энергию элемента. Полагая d{vo\)=rdQdr dz и используя (10.3) и (11.27), получим для потенциальной энергии л-й гармоники Пр (начальные деформации для простоты исключены)

-inj {P°n}, (11.28)

где для симметричных членов матрица жесткости имеет вид

а {Fn* } и {F?,} - соответственно векторы распределенных нагрузок и узловых сил для симметричного поведения. Аналогично члены с верхним индексом а определяют матрицы, отвечающие антисимметричному поведению. Следует заметить, что разложение выражений для этих матриц вряд ли приводит к появлению членов типа

J cosrtede = 5 sin2rtede = n,

позволяющие затем исключить окружную координату из выражения для интеграла.

Поэтому общая задача разбивается на отдельные задачи анализа симметричной и антисимметричной мод для каждой из гармоник. Реакция конструкции определяется как сумма соответствующих решений. Следует учесть, что при получении решений для компонент гармоник с /1=1 необходимо задать три условия закрепления, а при п>1 для обеспечения невырожденности глобальной матрицы жесткости необходимо зафиксировать лишь осевую моду движения тела как твердого целого. Для п=0 необходимо исключить вращение тела как твердого целого и смещение вдоль оси. Примеры применения описанного в этом разделе подхода приводятся в [11.8-11.10].

11.4. Заданное объемное изменение - несжимаемость

Обычной задачей механики грунтов является изучение отвердения. Эта задача характеризуется заданием изменения объема в грунте. В том случае, когда изменение объема равняется нулю, выполнены условия несжимаемости. В обоих случаях для анализа грунтов требуется модифицировать изложенные выше процедуры.

Анализ полностью насыщенных грунтов без дренажа, согласно линейной теории, предполагает, что рассматриваемый материал является двухфазной пористой средой. Одна фаза состоит из пористого материала с линейными упругими характеристиками, а другая фаза - сплошная несжимаемая жидкость. Предположим, что напряжения а° в первой фазе (пористом материале) связаны с деформациями е° обычным линейным законом

а =[Е ]8 . (П.30)

Коэффициенты упругости [Е ! заданы, а коэффициент Пуассона имеет значение, меньшее 0.5. Уравнения (П.30) представляют собой уравнения состояния для фильтрации в грунте. Систему уравнений жесткости можно построить при помощи соотношения (П.30), если преобразование от степеней свободы к деформациям соответствует типу используемого элемента. Однако наличие давления в порах для насыщенного состояния требует равенства нулю объемной деформации е т. е.

г =гх+гу+г,=0. (П.31)

Поэтому с учетом уравнений, связывающих перемещения и деформации, и обычных представлений перемещений через функции формы ( =LN J{u}, t=LN J{v} и w=iNj{w}) получим

= 0,

(П.32)

а так как требуется, чтобы изменение объема для каждого элемента равнялось нулю, то для отдельно взятого элемента будем иметь

5 e d(voJ)=.[Gf]

= 0,

d(vol).

(П.ЗЗ)

(11.34)

Уравнения (П.ЗЗ), очевидно, представляют собой ограничения, которые можно добавить к глобальной системе уравнений с помощью