2.3. Свойства соотношений между силами и перемещениями для элемента

Определим вид соотношений, связывающих узловые силы и узловые перемещения конечного элемента, т. е. так называемые соотношения между силами и перемеш/ениями. Соотношения между силами и перемещениями для элемента записываются в одном из трех основных видов: (1) уравнения жесткости, (2) уравнения податливости, (3) смешанные соотношения между силами и перемещениями.

Уравнения жесткости для элемента являются линейными алгебраическими уравнениями, которые записываются в виде

{Р}=[к{Л}. (2.1)

Матрица [к] - матрица жесткости элемента, а{Р}и{Л} - соответственно векторы сил н смещений для элемента. Заметим, что прямоугольная матрица обозначается символом [ 1. Отдельный элемент матрицы [к] назовем коэффициентом жесткости элемента. Если перемещение А; полагается равным единице, а перемещения, отвечающие остальным степеням свободы, полагаются равными нулю (Ah=0, кф1), значение силы f; равно k,j.

На рис. 2.6 для треугольного элемента изображен случай, когда перемещение, отвечающее степени свободы 1, полагается равным единице (т. е. А, = 1), а перемещения, соответствующие остальным степеням свободы, полагаются равными нулю (Аа=Дз = = . . .-=А =0). Следовательно, столбец узловых усилий равен столб-

нии, не является единственным способом достижения сходимости. Можно также сохранить размеры элементов и последовательно улучшать представления для полей в элементе. Элементы, которые отвечают более сложным представлениям полей по сравнению с простейшим для данного элемента полем, известны как элементы более высокого порядка.

При расчетах по методу конечных элементов источниками ошибок могут служить два условия: условие равновесия и условие непрерывности перемещений. В большинстве существующих моделей конечных элементов стараются удовлетворить условиям непрерывности перемещений, поэтому можно считать, что погрешности при численном анализе возникают из-за неточного удовлетворения условий равновесия. Полная процедура численного исследования методом конечных элементов позволяет, однако, считать, что возникающие погрешности обусловлены нарушением обоих условий. Как будет показано, теоретическое исследование метода конечных элементов тесно связано с выяснением, какое из условий выполняется, а какое нарушено.

цу коэффициентов матрицы жесткости, отвечающему Ai, откуда

(F}={ka} ( =1.....6),

{F)=iF,. . .F,J\ {k;,}=L*u. . A.J-

Очевидно, что Fi=ku - сила, обеспечивающая единичное смещение Al, а 2=21 и т. д.- реакции. Поэтому столбец коэффициен-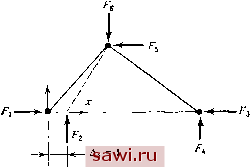

Рис. 2.6. Треугольный пластинчатый элемент.

тов матрицы жесткости {ка} представляет систему уреюновеиленных сил, действующих на элемент. Аналогичная интерпретация справедлива и для других столбцов матрицы жесткости элемента.

лг, ц

Рис. 2.7. Осевой стержневой элемент.

Рассматривая известные соотнощения для стержневого элемента, изображенного на рис. 2.7, получим пример матрицы жесткости элемента

1 -Г - 1 1

Соответствующее уравнение равновесия есть 2Fj.=0, что приводит к равенству нулю суммы элементов в каждом столбце.

Другим примером может служить простейший изгибаемый элемент, изображенный на рис. 2.8(a), для которого матрица жесткости может быть записана в виде (детали построения указанной матрицы

содержатся в разд. 5.2):

где угловые перемещения Qi=-dw/dx К, e-dciy/d; а. Как отмечалось в разд. 2.1, знак минус возникает потому, что вращениям в положительном направлении (по часовой стрелке) концевых точек элемента (6i, 63) отвечает отрицательное смещение w.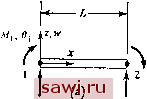

М2,в2

Рис. 2.8. Балочный элемент, (а) Элемент общего вида; (Ь) свободное опирание; (с) консольное закрепление.

При рассмотрении указанного алгебраического представления заслуживают внимания несколько аспектов. Во-первых, усилия, приложенные к элементу, суть непосредственно силы (fj, и моменты (All, Af 2), а перемещения отвечают поступательным {w, и вращательным (0i, 62) степеням свободы. Поэтому, если используются обобщенные понятия силы и перемещения, то эти понятия можно отнести не только непосредственно к силам и прямолинейным перемещениям, но также к моментам, и угловым перемещениям, высшим производным от перемещений (например, dwldx-) и связанными с ними силовыми параметрами и даже к обобщенным перемещениям и силам, не имеющим физического смысла.

Во-вторых, следует отметить, что условия равновесия сил, отвечающих каждому столбцу матрицы жесткости, определяются не только приравниванием нулю суммы элементов в указанном столбце. Сумма коэффициентов жесткости, соответствующих силам Fi, fa, действующим в направлении г, согласно условиям равновесия УРг= действительно равна нулю. Однако для оставшихся коэффициентов необходимо учесть уравнение равновесия для моментов. Для столбца 1, например, рассмотрев моменты относительно точки 2, получим 22=(6L-3L-3L)=0.

В-третьих, порядок задания компонент векторов сил и перемещений приводит к тому, что за всеми величинами, относящимися