Задачи

11.1. Постройте матрицу жесткости для кольцевого элемента, показанного в разрезе на рис. Р11.1, используя линейную радиальную функцию перемещений.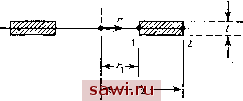

Рис. РИ.1.

11.2. Постройте матрицу жесткости кольцевого элемента, изображенного в разрезе на рис. 11.4, используя билинейную функцию перемещений.

11.3. Проверьте формулу (11.18Ь) для

11.4. Используя для перемещения и из (11.24) двучленное гармоническое разложение в ряд по симметричным членам (т. е. и\ и и\), постройте соответствующую матрицу жесткости кольцевого элемента из задачи 11.1.

11.5. Основываясь на функционале Рейсснера для плоско-напряженного состояния (см. (6.81)), получите выражение (11.38) для функционала П/ в случае несжимаемого материала.

11.6. Выведите дискретную форму для П/ (см. соотношение (11.38)) и преобразуйте полученную смешанную матрицу к матрице жесткости, предполагая, что параметры поля давления не связаны с параметрами этого поля соседних элементов.

11.7. Получите матричные уравнения для анализа обобщенного плоского деформированного состояния, используя описанный в конце разд. 11.1 подход.

11.8. Получите явный вид матрицы ID] из (11.27).

11.9. Постройте для несжимаемого упругого изотропного материала матрицу жесткости, основанную на девиаторных компонентах деформации. Используйте простой (с линейным полем перемещений) треугольный элемент при условиях плоской деформации.

11.10. Обобщите соотношения жесткости для плоской деформации (11.3) на случай учета начальных деформаций.

ИЗГИБ ПЛАСТИН

Много усилий затрачено на построение конечных элементов, моделирующих пластину при изгибе [12.11. Требованиям адекватной формулировки трудно удовлетворить, и по этой причине было предложено чрезвычайно широкое множество альтернативных формулировок. Поэтому строились улучшенные модели на основе более широкого использования вариационных принципов, нежели для других типов элементов. Однако и здесь основными были формулировки, базирующиеся на принципе минимума потенциальной энергии.

Значение изучения вопросов, касающихся изгиба плоских пластин, превосходит чисто утилитарные аспекты непосредственного построения элементов в рамках линейных статических формулировок, как это сделано в данной главе. Один из эффективных элементов конечно-элементного анализа тонких оболочек базируется на представлении их плоскими элементами. Такие элементы строятся с помощью суперпозиции свойств изгибаемых и плоско-напряженных элементов. Плоское напряженное состояние описывалось в гл. 9; данная глава завершает описание существенных аспектов анализа оболочек.

Важность понимания вопросов изгиба пластин вытекает также из практической ценности изучения динамических аспектов поведения и потери устойчивости пластинчатых и оболочечных конструкций. Последняя тема рассмотрена в гл. 13. При построении конечно-элементных уравнений, описывающих это явление, будем опираться на полученное в данной главе конечно-элементное представление.

И наконец, следует отметить, что упоминавшиеся выше трудности в выборе адекватных полей перемещений возникают из-за того, что изгиб тонких пластин описывается дифференциальным уравнением четвертого, а не второго порядка, как в случае плоских

И трехмерных задач теории упругости. Уравнениями четвертого порядка наряду с широким кругом физических задач описываются и другие задачи теории упругости, поэтому важно выяснить основные характерные трудности для каждой из них.

Этот вопрос был затронут потому, что трудности при выборе допустимых полей перемешений можно обойти, используя смешанные вариационные принципы и вариационные принципы, базирую-шиеся на рассмотрении функционала дополнительной работы, для которых минимальны требования при выборе полей напряжений, либо с помощью нзопараметрических трехмерных элементов, кото- рь1е описывают поведение тонких пластин при наложении определенных ограничении и выполнении других операций. Изопараметрические элементы изучались в гл. 9 и 10, первый подход обсуждается ниже.

В начале данной главы описывается наиболее простая ситуация, возникающая при изгибе пластин, т. е. изгиб в отсутствие сдвиговых напряжений и начальных деформаций. Кроме того, обсуждаемые формулировки и задачи в основном относятся к изотропным материалам. Вслед за кратким обзором основных соотношений теории изгиба пластин внимание уделено многочисленным альтернативным формулировкам для четырехугольных и треугольных элементов. В противоположность гл. 9 Плоско-напряженное состояние треугольные элементы здесь менее предпочтительны, нежели четырехугольные. Поэтому последние рассматриваются в первую очередь.

Во многих отношениях построение и стиль этой главы отличаются от построения и стиля других глав книги. Детальное описание операций по формулировке лишь небольшого числа из широкого разнообразия формулировок пластинчатых элементов при изгибе потребует объема целой главы. Наша же основная цель - дать всестороннее описание техники построения конечных элементов для изгибаемых пластин, и чтобы добиться этого, здесь принят обзорный стиль изложения. Однако некоторые основные аспекты проблемы рассматриваются подробно.

Подробно приводятся основные соотношения и выражения для энергетических функционалов изгиба пластин, благодаря этому можно выявить важную роль смешанных функционалов и функционала дополнительной работы. Весьма полно дается описание прямоугольных элементов. Пристальное внимание уделяется двум широко распространенным видам треугольных элементов. И наконец, рассматриваются деформации, вызываемые поперечными сдвигами. Этот аспект изгиба пластин важен сам по себе. Кроме того, на его основе можно предложить подходы описания изгиба без сдвига, которые более просты с точки зрения формулировки, нежели общепринятые подходы, базирующиеся на использовании допустимых полей перемещений.