12.1. Теория изгиба 12.1.1. Основные соотношения

Теория изгиба пластин подробно излагается во многих книгах (см., например, [12.2-12.4]), и ниже вкратце приводятся лишь необходимые соотношения для дальнейшего построения элементов.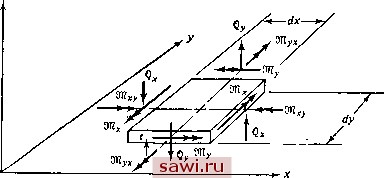

Рис. 12.1. Бесконечно малый элемент тонкой пластины

На рис. 12.1 изображен бесконечно малый элемент тонкой пластины толщины t. Пластина характеризуется плоским напряженным состоянием {Ог=Ухг=Ууг=Щ И, согласно обычным прсдполо-жениям изгиба пластин, напряжения линейно из.меняются по толщине. Интегрируя действующие в пластине напряжения по ее толщине, приходим к результирующим силовым характеристикам в виде изгибающих Шх, Шу и крутящего Шху моментов, отнесенных к единице длины. Векторы, отвечающие положительным значениям этих моментов, изображены на рис. 12.1. Для простоты на рисунке не показаны производные этих элементов и соответствующие им сдвиги, которые учитываются при формулировке дифференциальных уравнений равновесия. Имеем

(/2 </2

-1/2 -1/2

Шху = Шух= J Vdz.

-t/2

Удобно рассматривать строку усилий Ш=[ ШхШуШхукак аналог вектора напряжений о= Laoty для плоского напряженного состояния.

Основное предположение теории изгиба тонких пластин заключается в том, что отрезки, которые были первоначально перпендикулярны к срединной поверхности пластины, остаются перпендику-

лярными К ЭТОЙ поверхности и в процессе деформирования пластины. Производные угловых смещений этих нормалей определяют кривизны Хх, Ху и кручение ху поверхности. Предполагается, что они адекватно аппроксимируются вторыми производными функции поперечных смещений w:

дхду

(12.1)

где W отсчитывается от исходного состояния срединной поверхности пластины. Кривизны и кручение - главные меры деформации при изгибе тонких пластин. Следовательно, вектор кривизны >с= х ХуХу] является аналогом поля деформации e= exeyYyJ для плоского напряженного состояния.

Учитывая приведенные выше аналогии и определения, построим еще одну аналогию с плоской теорией упругости и введем уравнения состояния изгиба тонких пластин

9W = [E/]x, где для ортотропной пластины

[Е/] =

О D

(12.2)

(12.3)

Здесь Dx, Dy н Dl - изгибные жесткости ортотропной пластины. В более знакомо.м случае изотропной тонкой пластины

Г\ II О -

1 О , (12.3а)

О (l-fi)/2

[E/J = D

Определяющее дифференциальное уравнение равновесия изгиба пластин важно для понимания вопросов выбора полей перемещений в элементе. Основой для этого уравнения служат дифференциальные уравнения равновесия, которые выводятся путем рассмотрения равновесия сил, действующих на бесконечно малый элемент соответственно вдоль вертикальной оси и осей х и у. Следовательно, имеем

дх 5<г

f+ ? = 0, (12.5а)

дх дх ду

. = 0.

(12.5Ь) (12.5с)

где q - поперечная распределенная нагрузка, а Q. и d? - перерезывающие силы.

Теперь, подставив соотношения между моментами и кривизнами (12.2) в (12.5Ь) и (12.5с), а результирующие выражения - в (12.5а), получим

D.-f2(D.-f2D.,)3,-fD, = ,. (12.6)

Для пластины из изотропного материала это уравнение упрощается:

Заметим, что получение решения задачи изгиба тонких пластин с кинематической точки зрения полностью сводится к нахождению единственной компоненты перемещения w, т. е. прогибов.

12.1.2. Потенциальная жергня

Большинство существующих формулировок конечных элементов для изгибаемых пластин получаются на базе принципа минимума потенциальной энергии. Развивая аналогию с плоско-напряженным состоянием, получим

n=i-JxT[E/]xd/l-fV, (12.7)

где X и [£/] определены ранее, а V - потенциал прикладываемых нагрузок. В случае заданных распределенных нагрузок q, нормальных к поверхности пластины, указанный потенциал выражается формулой

- \qwdA, (12.8а)

а для заданных граничных усилий б?, изгибающих и скручивающих моментов да и¥, (рис. 12.2) потенциал равен

- J (aw+m e +s-Qs)dS, (12.8b)

где Sa - участок границы, где приложены указанные нагрузки. Наконец, для заданных усилий Рг. и моментов Л!;. и Му в узловых соединениях имеем

- S F,w,-i: M.,e - S м е (i2.8c)