где суммирование по t распространяется на все узловые соединения элемента.

Рисунок 12.3, на котором изображен прямоугольный пластинчатый изгибаемый элемент, поясняет вид сосредоточенных сил и моментов и соответствующих им перемещений. Основные предположения теории изгиба тонких пластин (сохранение нормали, пренебрежение сдвиговыми деформациями) приводит к тому, что наклон срединной поверхности и угловое смещение в каждой точке совпа-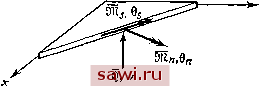

Рис. 12.2. Заданные граничные усилия.

дают. Поэтому Qx=\dw/dy\, By=-\dw/dx\. В выражении для 9у отрицательное значение производной обусловлено тем, что вращение в положительном направлении вокруг оси (см. рис. 12.3) вызывает отрицательные прогибы w. Следует также указать на различие между моментами в узлах, являющихся сосредоточенными моментами Мх, My, измеряемыми в единицах дюйм-фунт (или м-И), и распределенными моментами Шх, Шу, Шху, измеряемыми в единицах дюйм-фунт/дюйм. Узловые параметры искомого конечно-элементного представления суть сосредоточенные моменты (Мх-, Му и силы (Fz), а также соответствующие им перемещения.

С физической точки зрения очевидно, что поле перемещений конечного элемента при изгибе, как этого требует принцип минимума потенциальной энергии, должно быть непрерывно вместе со своими первыми производными при переходе границ элементов. Те же условия получают математически, анализируя выражение для функционала потенциальной энергии Пр, включающее вторые производные от w, что и обусловливает необходимость непрерывности первых производных. Этому требованию удовлетворить трудно. Поэтому при формулировке изгибаемых пластинчатых элементов оказались весьма привлекательными альтернативные вариационные принципы, требующие непрерывности лишь самой функции w.

Вид функционала потенциальной энергии показывает, что выбираемое поле должно быть по крайней мере квадратичньгм - в ре-

зультате взятия вторых производных исключается вклад всех линейных и постоянных членов полей перемещений. Как было показано для балки, обычно при описании изгиба используют кубические функции. Насколько этот подход эффективен для пластин, станет ясно из последующих разделов.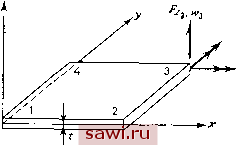

Типичные

узловые

усилия

Рис. 12.3. Изгибаемая тонкая прямоугольная пластина.

В качестве заключительного замечания, касающегося потенциальной энергии, отметим, что для изотропного материала уравнение (12.6) является уравнением Эйлера д.ля функционала потенциальной энергии. Значение этого обстоятельства заключается в том, что то же уравнение (с функцией напряжений Эри Ф в качестве неизвестной переменной) определяет растяжение пластины при применении формулировок, базирующихся на принципе минимума дополнительной работы. Следовательно, рассуждения, касающиеся выбора полей перемещений, непосредственно справедливы и для формулировок, соответствующих плоской задаче.

Уместно изучить процедуру дискретизации функционала потенциальной энергии при получении конечно-элементных соотношений между силами и перемещениями. Принимаемый подход очень близок процедурам из предыдущих глав. Выражение для выбранного поля перемещений сначала дифференцируется согласно (12.1) с целью отыскания поля х. В результате приходим к соотношениям вида

x=[D]{A}. (12.9)

Например, для изображенного на рис. 12.3 прямоугольного элемента

{Л}= L W, шз W, е е е е,;е е, е е, j \ (\2.щ

Подставляя (12.9) в выражение для энергии деформации, входящее в полную потенциальную энергию, получим

П,=Ц[к]{А} + К,

(12.7а)

[к] =

(12.11)

где, как и в предыдущих главах,

\[DY[E,][D]dA

Заметим, что предполагаемое поле перемещений фигурирует в оп-ределении величины V, если заданы распределенные нагрузки q, ё, Ш н 9Л ,

В тех случаях, когда предполагаемое поле представлено полиномиальным рядом, важно обратить внимание на определение величин 6 и 6j,. Имеем (см. разд. 8.2)

w=-lPim)J{a}, (12.12а)

поэтому

др (ш)

J{a}, e = -[j{ab (12.12b. с)

Следовательно, определяя (12.12) в узлах, приходим, как обычно, к полной системе уравнений вида

{Л}=[В1{а}. (12.13)

Разрешим это уравнение относительно {а} и подставим полученное выражение вновь в (12.12). Продифференцируем результирующие выражения согласно (12.1) и выпишем (12.9). Также можно продифференцировать выражение (12.12) непосредственно согласно соотношениям, связывающим кривизны и перемещения (соотношения (12.1)), и подставить полученный результат в выражение для энергии деформации. Получим основную матрицу жесткости, относящуюся к параметрам {а}. Матрица жесткости, соответствующая узловым перемещениям, получается в результате применения к основной матрице жесткости матрицы, обратной к [В] из (12.13), подобно тому, как преобразуются координаты. Ниже, в этой главе представится возможность проиллюстрировать эту процедуру.

12.1.3. Допопнитепьная >нергия

Дополнительная энергия упругой конструкции определяется в гл. 6 в терминах напряжений о=\ ахОуГху J. Теперь, используя аналогию, описанную в п. 12.1.1, можно построить выражение для дополнительной энергии при изгибе тонкой пластины. Имеем 11= = U* + V*, где в данном случае

и* =JШ[Ef]-ШdA (12.14)

и для распределенных и граничных нагрузок

V = -\q-wdA- (Qw + m -e + m,-Q,)dS. (12.15)

л Sa